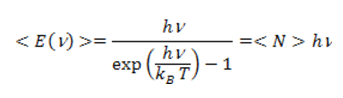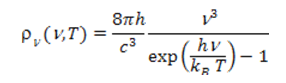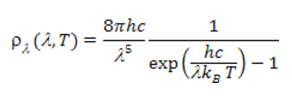La théorie de Planck

Toutes les tentatives pour expliquer le comportement de ρ_ν(ν,T) représenté sur la Figure 2 de l’article avec les concepts de la physique classique ont échoué. En effet, si l’on considère le cas particulier, permettant d’effectuer les calculs, d’une cavité cubique vide, à parois parfaitement réfléchissantes, de volume unité, il se produit un phénomène d’ondes stationnaires analogue à celui d’une corde vibrante fixée à ses deux extrémités. Dans une cavité un mode caractérise une onde électromagnétique stationnaire particulière donnée par sa fréquence ν, sa vitesse de propagation (ou célérité) c, sa direction de propagation, ainsi que par la direction et l’amplitude de son champ électrique. Les fréquences possibles sont discrètes et sont désignées par fréquences propres. Ces dernières  forment un spectre très serré caractérisé par une densité de modes (nombre de modes par unité de volume de la cavité) D(ν) proportionnelle à ν².

En théorie classique, l’énergie moyenne <E(ν)> d’une onde stationnaire assimilable à un oscillateur harmonique[1] est simplement k_BT où k_B est la constante de Boltzmann et T la température absolue. Ceci exprime le fait qu’à l’équilibre thermique  l’énergie se répartit uniformément dans tous les modes accessibles. La densité spectrale énergétique ρ_ν(ν,T)   donnée par le produit D(ν)<E(ν)> est alors proportionnelle à k_BTν². Ce résultat de la théorie physique classique, représenté sur la Figure 2 en pointillé, est appelé modèle de Rayleigh. En intégrant sur toutes les fréquences de 0 à ν, il conduit  à une densité d’énergie totale ρ  proportionnelle à k_BTν³. Celle-ci croît sans limite à haute fréquence conduisant à une énergie totale infinie,  donc inacceptable. C’est ce qu’on appelle la « catastrophe de l’ultraviolet » qui a conduit Max Planck à formuler son hypothèse des quanta évoquée plus haut.

L’énergie d’un mode est quantifiée : les seules valeurs de l’énergie possibles d’un mode de fréquence  ν  sont  E_n=nhν  où n est un nombre entier positif ou nul et h, la constante de Planck, qui est identique pour tous les oscillateurs. Un oscillateur dans un état d’énergie E_n   est équivalent à n quanta ou photons d’énergie hν . Les échanges d’énergie entre l’onde et la matière (atomes, molécules) s’effectuent ainsi de façon discrète par échange de  photons. En quantifiant ainsi l’énergie de chaque oscillateur, un calcul statistique[2] [3] montre que l’énergie moyenne de chaque oscillateur est donnée par

où <N> est le nombre moyen de photons du mode d’énergie hν à la température T. Pour les modes de basse fréquence, hν  petit  devant k_BT, on retrouve la loi classique <E>=k_BT. Ces modes contiennent beaucoup de photons. En revanche, l’énergie des modes chute exponentiellement dès que hν excède nettement k_BT et <N>  devient très petit devant l’unité. En multipliant l’énergie des modes par leur densité D(ν), on obtient la fameuse formule de Planck :

où c est la vitesse de la lumière dans le vide. La variation de ρ_ν(ν,T) en fonction de la fréquence ν  a été représentée sur la Figure 2 pour diverses températures. Cette formule est en accord remarquable avec l’expérience. Elle permet en outre d’obtenir les deux constantes h/c³ et h/k_B d’où l’on déduit la valeur de la constante de Planck h = 6,62617 x 10^-34 J s et celle de la constante de Boltzmann k_B  = 1,38066 x 10^-23 J/K, ce qui conduit à une évaluation inattendue du nombre d’Avogadro N_A=R/k_B=6,0221 x 10²³ mol^-1 en parfait accord avec sa valeur obtenue par d’autres méthodes (R constante des gaz parfaits, lire lien pression, température, chaleur).

En intégrant sur toutes les fréquences on obtient la densité d’énergie du corps noir ρ = αT⁴  ainsi que le flux Φ rayonné par unité de surface du corps noir donné par la loi de Stefan-Boltzmann Φ=σT⁴,  avec σ=2π⁵k_B⁴/(15c²h³). Ceci conduit à des résultats en  parfait accord avec l’expérience. Notons que si l’on exprime la densité énergétique spectrale en fonction de la longueur d’onde, la théorie de Planck conduit à[4]

Les courbes des Figures 4 et 5 sont représentatives de cette fonction et  la loi de Wien résulte de la position de son maximum.

Cette théorie de Planck publiée en 1901 fut le premier pas vers la quantification de la lumière confirmée par Einstein en 1905 qui a introduit explicitement la notion de photon pour expliquer l’effet photoélectrique. L’existence de niveaux d’énergie dans les atomes et les molécules a ensuite été proposée par Niels Bohr en 1913 pour expliquer les spectres de raies. La Mécanique Quantique qui régit tous les phénomènes microscopiques n’a été élaborée que de manière progressive dans les années 1920 notamment avec les contributions de Louis De Broglie, Erwin Schrödinger et Werner Heisenberg.

Références et notes

[1] Chaque mode est caractérisé par une solution du type E_z = E₀ cos(ω t) sink_xx, où z est la direction du champ électrique E, ω = 2πν  la pulsation de l’onde et k_x = 2π/λ   le vecteur d’onde selon la direction de propagation x. Une solution de ce type est analogue à celle d’un oscillateur mécanique tel qu’une masse m suspendue à un ressort et dont la force de rappel est proportionnelle à l’élongation x et dont le mouvement est décrit par une oscillation harmonique du type x = x₀ cos ω t.

[2] Elie Belorizky, Initiation à la Mécanique quantique, Dunod, Paris, 2003.

[3] Elie Belorizky, Introduction à mécanique statistique, Presse Universitaire de Grenoble, collection Grenoble sciences, 1992.

[4] Nous avons en effet la correspondance ν=c/λ et l’égalité des densités d’énergie   ρ_λ(λ,T) |dλ|= ρ_ν(ν,T) |dν|, soit :                      ρ_λ(λ,T) = ρ_ν(ν,T) |dν/ dλ| = ρ_ν( c/λ,T)  c/λ².