Déviation de la lumière par un prisme
PDF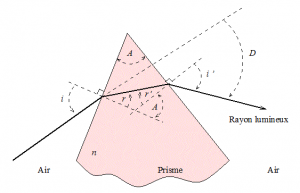
Un prisme d’angle au sommet A et d’indice n – l’air, d’indice unité, environne le prisme – dévie un rayon lumineux, dont l’angle d’incidence sur l’une des faces latérales du prisme est i, selon les lois de Snell-Descartes de l’optique géométrique : sin i = n sin r et n sin r’ = sin i’ (Figure 1 pour les notations). On a pour l’angle de déviation D = i + i’ – A, avec A = r + r’.
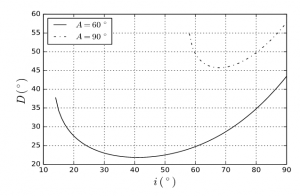
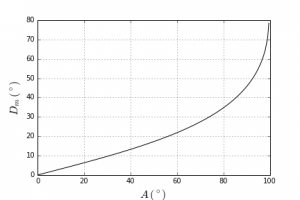
Le rayon lumineux ne peut émerger du prisme que si A < 2 a sin(1/n) ; pour la glace n = 1,31, d’où A < 99,5⁰. Si on trace la déviation D en fonction de i, on s’aperçoit qu’elle décroît vite, atteint un minimum minimorum correspondant à une traversée symétrique du prisme (i = i’), puis augmente lentement. Le minimum est très aplati, de sorte qu’un changement de l’angle d’incidence autour de l’incidence qui correspond à ce minimum n’en modifie pas notablement la valeur ; il s’ensuit une accumulation de lumière et donc une forte luminosité autour de ce minimum. Pour A = 60⁰, le minimum est de 22⁰ ; si A = 90⁰, il vaut 46⁰ (Figure 2). La figure 3 montre la valeur de ce minimum pour les différentes valeurs de A permises : elle augmente avec A.
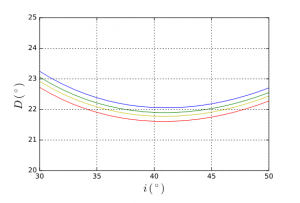
En outre, comme l’indice n dépend de la couleur du rayonnement incident, le minimum en dépend aussi ; un prisme décompose la lumière blanche en ses différentes composantes monochromatiques. C’est ce qui explique l’irisation des halos obtenus par réfraction. Pour A = 60⁰, on a un minimum voisin de 22⁰ qui croît du rouge au bleu (Figure 4)
Références et notes
Photo de vignette : iwannt via VisualHunt.com / CC BY




