Poussée d’Archimède et portance
PDF
Pour compenser leur poids les gigantesques cargos qui parcourent les océans bénéficient de la poussée d’Archimède. Mais pourquoi sont-ils aussi stables et ne se renversent-ils jamais, même lorsque la mer est démontée ? Par comparaison, les oiseaux, les avions et les planeurs, beaucoup plus lourds que l’air, semblent réaliser une performance extraordinaire en volant, comme le majestueux vautour de l’image de couverture. Nous allons voir que c’est leur mouvement qui engendre une force, appelée portance, capable de compenser leur poids.
1. Retour sur le poids et la poussée d’Archimède
Dès qu’il est lâché, le caillou tombe sur le sol, attiré par son poids. Sa chute s’arrête lorsque son appui sur le sol lui fournit une force exactement opposée à son poids, que l’on appelle la réaction de cet appui (lien vers l’article Les lois de la dynamique). Le caillou est de nouveau en équilibre.
Les corps plongés dans un milieu fluide, comme l’air ou l’eau, sont soumis sur leur périphérie à des pressions, dont l’effet global au repos se ramène à la poussée d’Archimède [1], égale et opposée au poids du fluide déplacé. Dans l’exemple du caillou lâché dans l’air, cette poussée est beaucoup plus faible que son poids, puisque la densité de l’air est environ 3000 fois plus faible que celle d’une pierre. Le caillou lâché accélère donc fortement, conformément à la loi fondamentale de la dynamique. En revanche, un ballon tombe plus lentement que le caillou et peut même s’élever s’il est gonflé avec un gaz plus léger que l’air, comme l’hélium ou l’hydrogène. Dans l’eau, le caillou tombe aussi mais beaucoup moins vite que dans l’air. Au début de sa chute, cela tient au fait que la poussée d’Archimède est encore incapable de compenser son poids, mais le déséquilibre des deux forces est modéré parce que la densité de l’eau n’est que 3 fois plus faible que celle d’une pierre. Puis, quand sa vitesse de chute devient significative, la pénétration du caillou dans l’eau se heurte à une résistance, appelée traînée, suffisante pour stopper son accélération et imposer une limite à sa vitesse de chute (lien vers l’article Résistance à l’avancement, ou traînée).
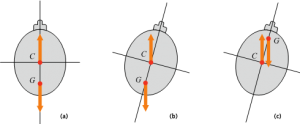
La situation est différente dans le cas d’un navire de surface immergé dans un ensemble de deux fluides : l’eau et l’air. On pourrait penser que l’air ne compte pas parce qu’il est presque mille fois plus léger que l’eau. Ce qui est vrai c’est que la poussée de l’air est négligeable par rapport à celle de l’eau. Mais il serait inexact d’oublier totalement l’air, qui intervient par l’existence de la surface libre. La partie immergée du bateau est limitée par la carène et par la portion de surface libre supprimée par la présence du navire, que l’on appelle la surface de flottaison. Ensemble, la carène et la surface de flottaison limitent le volume immergé V. Distinguons les deux parties de la poussée d’Archimède, celle qui s’exerce à bâbord et celle qui s’exerce à tribord. Toute inclinaison du navire détruit la symétrie de ces deux poussées, dans un sens tel qu’il tend à restaurer l’équilibre du navire. C’est ce qui distingue le cas d’un navire de surface de celui du sous-marin.

Ceci se traduit par l’existence d’un point qui n’a pas d’équivalent dans le cas des sous-marins, appelé le métacentre M, situé à la distance I/V au-dessus du centre de poussée C sur la ligne d’action de la poussée (verticale). Dans cette expression, I désigne le moment quadratique de la surface [3] de flottaison par rapport à son axe de symétrie. Lorsque le navire est soumis à de petites inclinaisons, le métacentre M demeure fixe et le point C décrit un arc de cercle de centre M et de rayon I/V. La condition de stabilité requiert que G soit au-dessous de M, et non pas de C. La différence par rapport au cas du sous-marin est importante : le navire peut être stable lorsque G est situé au-dessus de C, pourvu que le métacentre soit assez haut. Dans ces conditions, un sous-marin serait instable. Ceci exige que, toutes choses égales par ailleurs, la largeur l soit assez grande.
Une façon d’obtenir de grandes valeurs du rayon métacentrique I/V, de façon à garantir la stabilité du navire, consiste à doter celui-ci d’une double carène, dont aucune portion n’est proche de l’axe. Alors, presque toute la surface de flottaison étant éloignée de l’axe de symétrie, le rayon métacentrique peut devenir très grand. C’est le principe des catamarans. Les trimarans possèdent une carène principale assez vaste autour de l’axe, destinée à porter les équipements nécessaires à la navigation, mâts, voiles et cordages, mais aussi à abriter l’équipage, flanquée de deux carènes secondaires très légères à une certaine distance sur chacun des deux côtés. A l’équilibre, seule la carène centrale est partiellement immergée, mais une gîte modérée suffit à amener au contact de l’eau l’une des carènes latérales, qui trouve ainsi un appui supplémentaire, systématiquement stabilisant. Le couple de redressement dû à cette poussée latérale supplémentaire peut être important en raison de la longueur du bras de levier. Le trimaran représente donc une formule intermédiaire entre le navire monocoque et le catamaran, qui a l’avantage de devenir très stable pour des inclinaisons fortes.
3. La portance expliquée par le bilan des forces de pression
Qu’en est-il de ces objets volants comme les avions et les planeurs soumis à une poussée d’Archimède négligeable par rapport à leur poids puisqu’ils sont beaucoup plus lourds que l’air ? La force qui leur permet de s’envoler, puis de voler à une altitude fixée, que l’on appelle la portance, est encore la résultante des forces de pression sur leur périphérie. La nouveauté tient d’abord à la vitesse de ces objets : les avions à l’arrêt sur les aéroports ne peuvent pas s’envoler [4], ils ne parviennent à décoller qu’en roulant et après avoir dépassé une certaine vitesse.
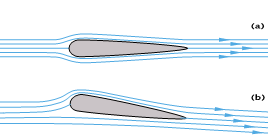
Par contre, lorsque l’aile possède une incidence non nulle, la symétrie est rompue comme le montre la Figure 3b : les lignes de courant se resserrent au-dessus de l’aile et s’écartent au-dessous. Le débit entre deux lignes de courant devant rester constant, la vitesse est d’autant plus grande que les lignes de courant se resserrent. La vitesse de l’air est ainsi plus faible le long de l’intrados que le long de l’extrados. Or, pour ralentir ainsi les particules fluides qui passent le long de l’intrados, il faut bien qu’une résistance s’exerce sur elles. Cette résistance à leur avancement est produite par une surpression qui prend place le long de l’intrados et ralentit localement l’air en le repoussant vers le bas. Il en résulte que la pression le long de l’intrados l’emporte sur celle qui s’exerce sur l’autre face, et que le bilan de ces pressions sur toute la surface de l’aile fait apparaître une force verticale non nulle. L’aile est alors soumise à une portance [5] liée à la vitesse de l’aile et à son incidence.
Dans le cas d’une aile d’avion, l’incidence est imposée par le pilote qui, pour décoller, alors que l’avion roule déjà à une vitesse suffisante, oriente vers le bas les volets arrière. Même s’il ne modifie pas l’incidence de l’aile toute entière, le pilote détruit ainsi la symétrie entre intrados et extrados, et c’est ce qui permet à la portance de se développer et de pouvoir l’emporter sur le poids. Inversement, pour diminuer l’altitude avant l’atterrissage, le pilote réduit l’incidence en remontant les volets arrière pour réduire la portance, voire la rendre négative et faire en sorte qu’elle s’ajoute au poids. Dans le cas d’un oiseau, c’est cet animal qui fait l’effort musculaire nécessaire à l’apparition de l’incidence et de la portance.
Le fait que l’aile ait une certaine épaisseur a pour effet de réduire l’efficacité de ce mécanisme, mais sans en compromettre le principe. En aéronautique, on parle de la finesse d’une aile pour qualifier sa minceur. Les voiles d’un bateau constituent de bons exemples d’ailes minces. Elles sont par ailleurs courbées par le vent qui les gonfle, ce qui accentue encore la dissymétrie et renforce le bilan des pressions, sorte de portance horizontale transmise au bateau par le mât. La combinaison de cette portance sur la voile et de celles exercées par l’eau sur le gouvernail – une autre aile mince – et éventuellement sur la quille – une troisième aile mince – permet même de naviguer par vent contraire. Le becquet arrière des voitures de compétition est aussi conçu pour être soumis à une portance, mais négative celle-ci, c’est à dire dirigée vers le sol comme le poids, de façon à augmenter la tenue de route du véhicule.
4. La portance expliquée par la présence d’un tourbillon
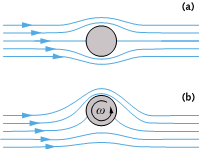
Imaginons maintenant que ce ne soit pas le cylindre tout entier qui tourne, mais seulement une couche pelliculaire, une sorte de peau plaquée sur son contour. Pour l’écoulement du fluide ambiant, qui ne ressent que cette peau, le résultat est le même. Le cylindre muni de cette peau mobile est soumis à une portance dont le signe dépend du sens de rotation de la peau.

Un tourbillon apparaît donc nécessairement autour de l’aile, lors du décollage. Or, initialement, aucun tourbillon n’était présent. Et cette grandeur est invariante sur des durées courtes par rapport au temps caractéristique du frottement visqueux. Un autre tourbillon, de sens opposé et de même intensité que celui qui engendre la portance, est donc aussi créé, mais celui-ci n’entoure pas l’aile et nous allons voir qu’il ne suit pas l’avion et reste au point de départ.
5. La portance sur une aile d’envergure finie



La formation en V des groupes d’oiseaux migrateurs (Figure 8) s’explique par le fait que chacun d’eux, excepté le premier, se place dans le courant ascendant du tourbillon marginal de celui qui le précède. Il fait ainsi l’économie d’une partie des efforts nécessaires pour maintenir son altitude. À tout objet ou animal soumis à une portance (avion, planeur, oiseau ou voile) est donc associée la formation d’une très grande structure tourbillonnaire, en forme de long tube refermé sur lui-même. Cette structure s’allonge régulièrement pendant toute la durée du vol. Son intensité est liée à la portance et son énergie est prélevée sur celle fournie à ces objets ou dépensée par ces oiseaux.

Les balles et les ballons sont des exemples d’objets volants de très petite envergure. La portance liée à l’existence d’un tourbillon permet d’expliquer leurs trajectoires parfois étonnantes, comme celles des balles de tennis ou de ping-pong, plus ou moins bombées par le mouvement de la raquette. Lorsque la raquette brosse la balle en passant par dessus, la trajectoire est fortement bombée vers le haut. La balle est dite liftée (du mot anglais lift qui désigne la portance) ; elle est dite coupée ou slicée (du mot anglais slice, tranche) lorsque la raquette brosse la balle en passant par dessous. La trajectoire courbée dans le plan horizontal du ballon de football qui, parti du point de corner, pénètre directement dans la cage du gardien de but est un autre exemple.

Références et notes
Photo de couverture : vol plané d’un vautour fauve illustrant l’existence d’une portance capable de compenser son poids. [Source : Diverticimes]
[1] Archimède, né à Syracuse vers 287 av. J.C. et tué lors du siège de cette ville en 212 av. J.C., est l’un des grands scientifiques de l’Antiquité grecque. Ses principales découvertes portent sur la statique et l’hydrostatique. Deux d’entre elles portent encore son nom : la poussée d’Archimède et la vis d’Archimède.
[2] Le centre de gravité d’un volume est son centre de masse, ou barycentre, dans l’hypothèse où il serait rempli d’un milieu homogène. Le centre de gravité d’une surface est défini de la même façon, mais à deux dimensions.
[3] Toute surface plane possède deux axes principaux orthogonaux passant par son centre de gravité. Dans le cas de la surface de flottaison d’un navire, ce sont l’axe de symétrie qui va de la proue à la poupe et l’axe perpendiculaire. Le moment quadratique par rapport à chacun de ces axes s’exprime de façon générale par une intégrale ; il est souvent dénommé moment d’inertie. Dans le cas particulier d’un rectangle de grand côté L et petit côté l, l’expression du moment quadratique par rapport au grand axe est Ll3/12. Dans le cas d’un navire de surface, si le volume de la carène peut être approché par Llh, où h est proportionnel au tirant d’eau, le rayon métacentrique a pour expression MC = l2/12 h.
[4] L’envol des hélicoptères, des oiseaux et des insectes est dû au mouvement de leurs pales ou ailes, rotation pour les premiers, battement rapide pour les seconds, ce qui constitue une différence majeure par rapport aux avions, dont les ailes demeurent immobiles. Le décollage vertical de certains avions de chasse résulte d’une autre poussée exercée par le jet issu des réacteurs.
[5] La théorie de cette portance, due aux mécaniciens des fluides Martin Wilhelm Kutta, allemand (1867-1944), et Nikolaï Joukowsky, russe (1847-1921), aboutit à la formule de Kutta-Joukowsky pour la portance : P = ρVΓ, où ρ désigne la masse volumique du fluide, V sa vitesse au loin et Γ la circulation de la vitesse sur le contour fermé de l’aile.
[6] L’intensité du tourbillon est le flux du vecteur tourbillon (rotationnel de la vitesse) à travers la section droite de l’aile. Cette grandeur est égale à la circulation de la vitesse sur le contour de l’aile, introduite dans la note [5] et notée Γ.
[7] Cette moyenne de la vitesse sur le contour de l’aile est proportionnelle à une grandeur importante : la circulation de la vitesse sur ce contour fermé Γ, qui est d’ailleurs égale à l’intensité du tourbillon.
[8] On prendra garde à ne pas confondre ces longs tubes nuageux, éventuellement présents sur l’axe des tourbillons marginaux, avec les grandes traînées bien visibles dans le sillage des avions à réaction. Ces dernières sont dues à la condensation de l’importante quantité de vapeur d’eau issue de la combustion et éjectée par la tuyère à l’aval des réacteurs. Ces signatures aériennes du passage d’un avion à réaction sont toujours visibles, même dans un anticyclone puissant et dans un air sec.
[9] Dans le vocabulaire marin, toute section de la carène perpendiculaire au grand axe est appelée couple et la plus grande d’entre elles est appelée le maître couple.
L’Encyclopédie de l’environnement est publiée par l’Association des Encyclopédies de l’Environnement et de l’Énergie (www.a3e.fr), contractuellement liée à l’université Grenoble Alpes et à Grenoble INP, et parrainée par l’Académie des sciences.
Pour citer cet article : MOREAU René (20 septembre 2018), Poussée d’Archimède et portance, Encyclopédie de l’Environnement. Consulté le 23 avril 2025 [en ligne ISSN 2555-0950] url : https://www.encyclopedie-environnement.org/physique/poussee-darchimede-portance/.
Les articles de l’Encyclopédie de l'environnement sont mis à disposition selon les termes de la licence Creative Commons BY-NC-SA qui autorise la reproduction sous réserve de : citer la source, ne pas en faire une utilisation commerciale, partager des conditions initiales à l’identique, reproduire à chaque réutilisation ou distribution la mention de cette licence Creative Commons BY-NC-SA.








