Les modèles de prévision météorologique

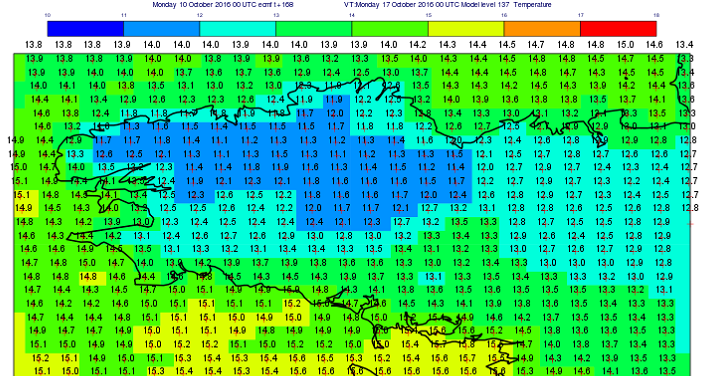
Cet article présente les principes de base de la modélisation numérique de l’atmosphère. Il explique d’abord comment on passe des équations générales et continues de la mécanique des fluides à une version discrétisée de ces équations. Puis il montre comment on peut les traduire en programmes informatiques à haute performance, les modèles atmosphériques, qui calculent l’état futur de l’atmosphère à partir d’un état initial construit en utilisant les observations météorologiques.  Le modèle atmosphérique est ainsi le maillon central des systèmes opérationnels de prévision numérique du temps.

 

1. Qu’est-ce qu’un modèle atmosphérique ?

Un modèle atmosphérique est un système informatique qui simule le comportement de l’atmosphère. Il est utilisé soit comme un laboratoire numérique pour étudier les processus atmosphériques et mieux les comprendre, soit comme un outil d’aide à la prévision du temps ou du climat.

Les lois de base qui décrivent l’évolution de l’état de l’atmosphère sont celles de la mécanique des fluides. Elles expriment l’évolution dans le temps d’un fluide (liquide ou gaz) à partir de son état initial supposé connu. Leur forme générale est universelle et donc valable dans des contextes très différents, par exemple l’écoulement de l’air autour d’un avion, la circulation de l’eau dans des tuyauteries ou dans les rivières, la propagation des ondes sonores autour d’une éolienne, ou encore l’ascension de la fumée issue d’une cheminée. Ces équations permettent aussi, et c’est ce qui nous intéresse pour les modèles atmosphériques, de décrire l’évolution des fluides géophysiques que sont les océans et l’atmosphère.

Dans le cas de l’atmosphère, les lois de la mécanique des fluides sont formulées pour prévoir les paramètres atmosphériques tels que le vent, la température, la pression et l’humidité. Ce sont des équations très complexes car il existe de nombreuses interactions croisées entre ces paramètres. Ces équations font également intervenir des processus à des échelles très différentes, de l’échelle de la planète à celle de la goutte de pluie, ainsi que les interactions avec la surface sous-jacente (sol, mer, couverture végétale, lien vers article Balsamo) et l’espace. Leur extrême complexité, due notamment à leur non-linéarité, exclut que l’on puisse les résoudre de façon analytique. La seule issue consiste donc à utiliser des techniques numériques approchées pour calculer l’évolution d’un état initial. Cet état initial qu’on appelle l’analyse est lui-même fabriqué  grâce à des méthodes mathématiques et numériques très sophistiquées d’assimilation des observations atmosphériques (lire Assimilation des données météorologiques).

Le fluide atmosphérique est essentiellement un gaz constitué d’air sec (20% d’oxygène, 80% d’azote) et de vapeur d’eau. D’autres gaz tels que l’ozone ou le dioxyde de carbone sont présents avec de très faibles concentrations (lire L’atmosphère et l’enveloppe gazeuse de la Terre). Ces gaz minoritaires jouent cependant un rôle essentiel dans le bilan énergétique de l’atmosphère. Dans la couche où ont lieu la plupart des  phénomènes météorologiques, la troposphère, les conditions de température et de pression peuvent entraîner des changements de phase de l’eau. La vapeur d’eau peut ainsi se transformer en condensats liquides ou glacés  qui constituent les nuages et les précipitations. La prise en compte de ces changements de phase, phénomènes à seuils très non-linéaires et donc difficiles à traduire en équations, est cependant essentielle pour modéliser correctement le comportement de l’atmosphère.

Dans le contexte de la prévision numérique du temps (PNT) (lire Introduction à la prévision météorologique), le modèle d’atmosphère est un des maillons du cycle « assimilation des données – calculs – prévision »mis en œuvre dans les centres de prévision opérationnels. Il doit non seulement produire des prévisions de bonne qualité, mais aussi être rapide et robuste afin de produire à temps et sans faute les informations nécessaires pour les prévisionnistes.

2. Les équations de la mécanique des fluides

Le système des équations d’Euler, qui exprime les principes fondamentaux de la mécanique et de la thermodynamique des fluides,constitue la base d’un modèle d’atmosphère. Ces équations ne s’appliquent pas à une molécule de gaz mais à une parcelle d’air. Celle-ci est supposée à la fois assez grande pour contenir suffisamment de molécules pour que les paramètres statistiques tels que la température et la pression puissent être définis et suffisamment petite pour être assimilée à un point dans l’immensité du milieu atmosphérique.

Ce système contient trois équations principales :

• L’équation mécanique qui exprime l’accélération du mouvement d’une parcelle d’air en fonction des forces qui lui sont appliquées. Dans un plan horizontal, cette équation donne l’accélération du vent en fonction des forces de pression et de la force d’inertie de Coriolis due à la rotation de la Terre. Sur la verticale, l’accélération du mouvement est contrôlée par la gravité et par la force d’Archimède.
• L’équation de la conservation de l’énergie totale qui, combinée à l’équation pour l’énergie cinétique déduite de l’équation du mouvement, fournit une équation pour la température (ou une autre quantité dérivée de la température comme l’enthalpie ou l’entropie). Elle décrit en particulier les effets sur la température du rayonnement solaire, du rayonnement infra-rouge émis par la Terre ou les nuages, et ceux associés à tout changement d’état de l’eau (l’évaporation refroidit, la condensation réchauffe).
• L’équation de conservation de la masse qui assure la conservation des différents constituants d’une parcelle d’air.

Á ces trois équations, on ajoute l’équation d’état des gaz qui relie les trois paramètres thermodynamiques, température, pression et masse volumique ainsi que les lois thermodynamiques décrivant les changements de phase de l’eau.

Les équations d’Euler sont capables, par exemple, de décrire chaque petit tourbillon au voisinage de la surface terrestre ou chaque contournement des filets d’air autour d’un obstacle. Mais la capacité des ordinateurs qui vont nous permettre de résoudre ces équations n’est pas encore suffisante pour, en pratique, calculer l’évolution de tous ces petits détails. Il est donc nécessaire de simplifier les équations d’Euler afin de ne conserver que les termes essentiels pour la météorologie.  La première étape de la simplification est de moyenner les équations originales dans le temps et dans l’espace afin de filtrer les processus rapides et de petite échelle spatiale qu’on ne peut pas décrire. Suite à cette opération de moyenne, les paramètres atmosphériques comme le vent ou la température qui sont prévus par les équations ne représentent plus le vent ou la température d’une petite parcelle d’air mais la moyenne de ces paramètres dans un volume suffisamment grand pour contenir un grand nombre de petit tourbillons et suffisamment petits pour que les paramètres moyennés contiennent encore la variabilité nécessaire pour décrire les phénomènes météorologiques que l’on veut prévoir (figure 1).

Dans une seconde étape, on analyse l’ordre de grandeur de chacun des termes des équations afin d’éliminer ceux qui deviennent négligeables aux échelles encore décrites par les équations moyennes. Par exemple, une approximation classique dans les modèles atmosphériques est l’approximation hydrostatique qui revient à négliger l’accélération verticale devant les deux forces qui interviennent dans l’équation verticale du mouvement, la gravité et la force d’Archimède, forces qui sont presque en équilibre dans l’atmosphère. En conséquence, les paramètres moyens décrits par les équations hydrostatiques (aussi connus sous le nom d’équations primitives) sont, par construction, toujours en équilibre hydrostatique. Autrement dit, dans un tel modèle, l’ajustement à l’équilibre hydrostatique est un processus très rapide qui, filtré par la moyennes patio-temporelle, n’est plus décrit explicitement pas ces équations. Les équations hydrostatiques ont en particulier la propriété de ne plus représenter la propagation verticale des ondes acoustiques, tellement rapides qu’elles n’ont que peu d’intérêt direct pour la météorologie. Leur filtrage est, par ailleurs, un avantage pour la stabilité des modèles numériques (voir section 3). Cette approximation hydrostatique s’avère valable tant que l’on moyenne les paramètres atmosphériques dans des volumes de section horizontale supérieure à quelques kilomètres. Par contre, pour des représentations plus fines, il peut devenir important de décrire explicitement les processus transitoires non-hydrostatiques.

L’opération de filtrage, si elle fait disparaître la possibilité de résoudre chaque petit détail du fluide atmosphérique par les équations,  laisse la possibilité de représenter l’influence collective que ces fluctuations ont sur les champs moyens. Cette possibilité est particulièrement importante pour tenir compte des échanges avec les surfaces terrestres sous-jacentes (lien vers article Les modèles de biosphère, hydrosphère et cryosphère), qui font intervenir des processus d’échelles très fines et très rapides de type turbulent. Des lois de régression statistiques qui ont pu être établies et validées par l’expérience permettent de relier l’effet collectif des petits tourbillons et des micro-circulations dans les premières centaines de mètres au-dessus de la surface à l’évolution moyenne du vent, de la température et de l’humidité dans cette couche. Ces lois statistiques sont à la base de petits modèles, intégrés au modèle global, que l’on appelle des paramétrisations physiques.

Les changements de phase de la vapeur d’eau en gouttelettes ou cristaux de glace qui peuvent ensuite s’évaporer ou fondre ne peuvent pas être décrits explicitement par les équations moyennées. Pour les représenter, à nouveau, il faut adopter une autre famille de paramétrisations basées sur des descriptions statistiques du comportement de populations de gouttes ou de cristaux qu’on appelle les schémas de microphysique des nuages.

Le modélisateur rencontre une difficulté supplémentaire pour représenter les nuages qui sont trop petits pour être créés par les ascendances dues à la vitesse verticale moyenne. Des paramétrisations spécialisées pour décrire les nuages de faible extension horizontale tels que les cumulus ou les cumulonimbus traitent à la fois les fluctuations de vitesse verticale et les changements de phase de l’eau. Ces paramétrisations, connues sous le nom de schémas de convection, sont un des éléments clés pour représenter correctement les échanges énergétiques dans les régions  tropicales et ainsi assurer le maintien des équilibres climatiques dans le modèle.

Il est également nécessaire de paramétrer l’ensemble des interactions entre l’atmosphère d’une part et, d’autre part, le rayonnement solaire qui vient de l’espace et le rayonnement infra-rouge qui est principalement émis par la surface terrestre. Ces effets doivent être largement simplifiés pour rendre la paramétrisation du rayonnement compatible avec les contraintes de production des prévisions dans les centres opérationnels.

Par habitude, les modélisateurs du système atmosphérique séparent les termes des équations qui s’expriment directement en fonction des paramètres moyens dans un sous-système, qu’on appelle la dynamique, des termes qui nécessitent le développement de paramétrisations placés dans un second sous-système qu’on appelle la physique. C’est le couplage entre ces deux sous-systèmes qui constitue un modèle d’atmosphère.

3. Discrétisation et algorithmes numériques

Les schémas numériques qui permettent de résoudre le système des équations moyennées sont basés sur une représentation discrète de l’atmosphère. Ils permettent de calculer les états successifs des paramètres atmosphériques définis à l’intérieur de chaque maille d’une grille tridimensionnel (figure 2).  La taille de la maille définit les résolutions horizontale et verticale du modèle et doit être consistante avec l’échelle caractéristique de l’opérateur de moyenne qui a été appliqué aux équations.

La résolution des équations ne se fait pas de façon indépendante pour chaque maille. En effet, l’expression des variations horizontales et verticales des diverses grandeurs ainsi que celle du transport de ces grandeurs par le vent, font intervenir des valeurs dans les mailles voisines. Les paramétrisations, elles, font souvent intervenir des calculs le long de toutes les mailles d’une colonne verticale (pour décrire par exemple la chute de la pluie ou le transport turbulent vers le haut de la vapeur d’eau qui s’évapore à la surface de l’océan).

La discrétisation des équations n’a pas lieu uniquement dans l’espace mais également dans le temps. Le pas de temps, qui est l’équivalent pour le temps de la taille de la maille dans l’espace, sépare deux estimations successives de l’état de l’atmosphère par le modèle (figure 3).

Les schémas numériques, même les plus sophistiqués, sont des méthodes de résolutions approchées dont la solution converge vers la solution exacte lorsque la résolutions patio-temporelle du modèle devient très fine. C’est pour cette raison que la résolution des modèles augmente au fur et à mesure que la capacité des calculateurs le permet.

Il faut s’assurer que le niveau d’erreur reste stable au cours de la simulation. Certains schémas numériques peuvent en effet voir leur erreur croître très rapidement si certaines conditions ne sont pas respectées. Une contrainte classique de stabilité, connue sous le nom de condition de Courant-Friedrich-Levy  ou condition CFL [1] spécifie que le vent dans une maille ne doit pas transporter l’air présent dans cette maille de plus de la taille d’une maille en un pas de temps. Si cette condition n’est pas vérifiée dans un schéma, l’erreur grossit jusque à atteindre des nombres infiniment grands, le schéma devient instable, on dit que le modèle explose.

De nombreux schémas de modélisation ont été proposés dans le passé et de nouveaux schémas sont encore publiés chaque année. La difficulté pour le modélisateur est de faire les choix qui permettent le meilleur compromis entre précision, stabilité et efficacité en temps de calcul. Ces choix ne sont pas indépendants de l’architecture du calculateur qui va être utilisé.

Même si tous les modèles reposent à la base sur le même système d’équations, en pratique, chaque implémentation peut varier largement d’un modèle à un autre. Suivant les directions horizontales, il existe une grande variété de maillages possibles (figure 4) qui va d’un simple découpage régulier le long des cercles de latitude et des méridiens à des grilles avec des mailles hexagonales ou triangulaires. Certains maillages plus étranges, comme la sphère-cube ou la grille Yin-Yang ont des propriétés mathématiques intéressantes, en particulier, elles ne présentent pas de singularité aux niveaux des pôles. Dans certains cas, le type de grille est imposé par la méthode numérique choisie. Le modèle global de Météo-France et le modèle du Centre Européen de Prévision Météorologique à Moyen Terme (CEPMMT) utilisent une transformation mathématique qui projette les champs de paramètres sur une base de fonctions mathématiques, les harmoniques sphériques. Pour que cette transformation soit précise, il est nécessaire d’utiliser une grille dite de Gauss [2]. À Météo-France, la grille est en plus étirée de façon à augmenter la résolution sur la France.

Dans la direction verticale, certains modèles découpent l’atmosphère avec des niveaux définis avec l’altitude, d’autres utilisent la pression pour définir le maillage vertical. Souvent, les niveaux ne sont pas strictement horizontaux mais ils suivent la forme du relief, au moins dans les couches les plus basses du modèle (figure 5).

En plus des modèles globaux qui produisent des prévisions pour l’ensemble de l’atmosphère et qui ont aussi souvent une version utilisée pour les prévisions à longue échéance, comme les prévisions saisonnières ou climatiques, il existe de nombreux modèles régionaux qui font les calculs uniquement sur une région donnée. La réduction du nombre de points de calcul dans ces modèles à aire limitée permet d’augmenter la résolution et d’optimiser les paramétrisations pour cette région. Une des limitations des modèles régionaux est la nécessité de coupler la solution sur les bords du domaine limité avec la solution fournie par un modèle global de résolution plus faible. Les techniques de couplages sont des sources d’erreurs importantes qui se propagent à l’intérieur du domaine d’intérêt et limitent ainsi la durée de ce type de prévisions.

Les champs prévus par le modèle ne sont pas stockés à chaque pas de temps mais uniquement pour les échéances requises par les utilisateurs. Les champs de paramètres bruts tels que la température, le vent ou l’altitude géopotentielle sont interpolés sur les niveaux isobares classiquement utilisés par les prévisionnistes. La couverture nuageuse et les précipitations en surface sont fournies directement par les paramétrisations des nuages. De nombreux autres paramètres sont diagnostiqués à partir des sorties brutes du modèle afin d’aider le prévisionniste à analyser au mieux le comportement de l’atmosphère et à comparer les états prévus avec les nouvelles observations qui arrivent en temps réel. On produit ainsi des cartes de paramètres en surface comme la température à une altitude de 2 m, le vent à 10 m, les rafales, mais aussi des images satellites ou des images radar synthétiques (figure 6). Les sorties de modèles constituent l’information principale qui est mise à disposition des experts prévisionnistes (lire Le rôle du prévisionniste). Le travail d’interprétation de l’ensemble de ces produits permet de choisir un scenario pour l’évolution du temps dans les jours à venir et d’affiner ce scenario pour chaque région.

4.  Le défi des programmes informatiques et des supercalculateurs

Les modèles de prévision opérationnels en 2016 comportent plusieurs millions de mailles, une dizaine de variables par maille et des pas de temps de quelques minutes. Ils imposent de résoudre plus de 100 millions d’équations complexes pour produire une seule heure de prévision. Seule l’utilisation des calculateurs les plus puissants, mais aussi d’algorithmes efficaces permet de produire des prévisions suffisamment rapidement pour qu’elles puissent être transmises aux prévisionnistes en temps utile.

Une des clés du calcul rapide est d’arriver à distribuer les calculs afin de faire travailler en parallèle les différents processeurs d’un supercalculateur. Et cette parallélisation doit se faire avec des communications minimales entre processeurs car ces communications sont souvent beaucoup moins rapides que les capacités de calcul local des processeurs. Ces contraintes technologiques en constante évolution imposent aux modélisateurs d’adapter en permanence les schémas numériques aux nouvelles spécificités des calculateurs. Des tests comparatifs sont régulièrement réalisés pour évaluer l’efficacité des modèles en termes de vitesse de calcul (figure 7) à la fois pour la technologie des calculateurs actuels mais aussi en projection pour les possibles technologies à venir.

Le modèle d’atmosphère est donc finalement un code informatique de plusieurs millions de lignes, développé et maintenu par des dizaines de personnes en parallèle. Il est le maillon central du cycle d’assimilation des données et de prévision à haute résolution dans les centres de prévision météorologique opérationnels. Il est aussi utilisé pour produire les prévisions perturbées de chaque membre de la prévision d’ensemble (lire La prévision d’ensemble). Couplé à un modèle d’océan, il sert pour les prévisions mensuelles, saisonnières et pour monitorer l’évolution du climat (lire La prévision saisonnière).

La modélisation numérique de l’atmosphère a dû et doit continuer à faire face à :

• l’augmentation de la résolution et donc du nombre de calculs,
• l’augmentation des processus que l’on veut décrire (par exemple, ajout de la chimie atmosphérique),
• l’augmentation du nombre de processeurs dans les calculateurs,
• l’augmentation de la consommation électrique des supercalculateurs,
• l’augmentation du nombre de lignes des programmes,
• l’augmentation de la masse des données à traiter et à stocker en sortie.

Un enjeu important des années à venir consiste à améliorer la scalabilité des modèles existants, c’est à dire leur capacité à s’adapter à toutes ces augmentations, tout en restant des outils utilisables par l’ensemble des chercheurs-développeurs et utiles pour les applications de prévision du temps.

 

---

Références et notes

Image de couverture : Prévision des températures sur la Bretagne effectuée le 10 octobre 2016 pour le 17 octobre à 00 GMT par le modèle numérique du CEPMMT (chiffres en noir : températures en °C ; croix rouges : centres des mailles).

[1] J. Coiffier : Éléments de prévision numérique du temps, « Cours et Manuel », 1997, Météo-France.

[2] S. Malardel, N.Wedi, W. Deconinck, M. Diamantakis, C. Kuhnlein, G. Mozdzynski, M. Hamrud, P. Smolarkiewicz : A new grid for the IFS, 2016, ECMWF Newsletter 146.

[3] S. Malardel : Fondamentaux de Météorologie, 2^nd éd., 2009, Cépadues éditions.