La prévision d’ensemble

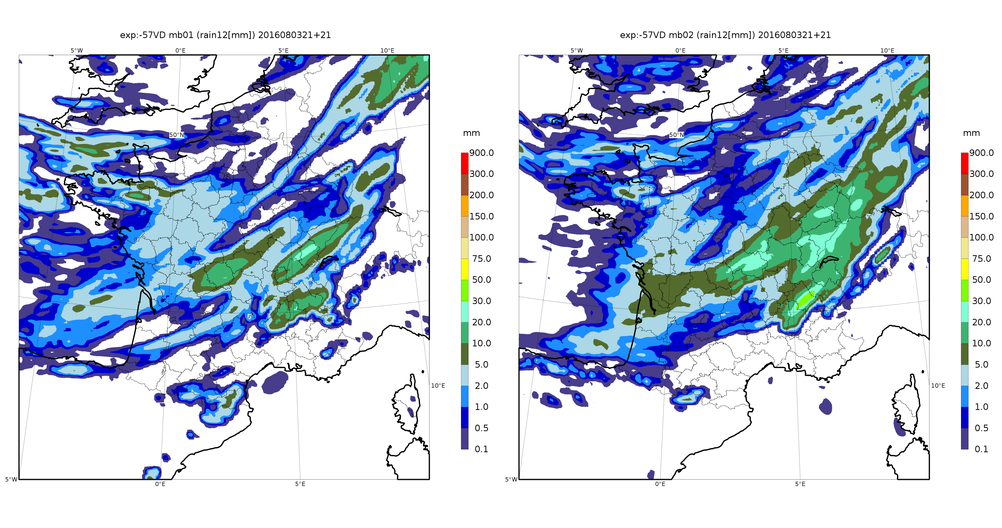
La prévision d’ensemble est l’outil qui permet de faire des prévisions météorologiques probabilistes. C’est à la fois une alternative et un complément devenu indispensable à la prévision déterministe du temps. Elle consiste à simuler par tirage aléatoire les erreurs commises lors du calcul d’une prévision numérique du temps pour aboutir à l’évolution la plus probable. Ces erreurs inévitables peuvent provenir d’inexactitudes dans les valeurs retenues pour caractériser l’état initial de l’atmosphère, ou bien d’approximations effectuées dans les équations, ou encore des incertitudes acceptées dans la modélisation des conditions aux interfaces sol/air ou mer/air.

1. Intérêt et principe de la prévision d’ensemble

A partir d’observations, un modèle (par exemple, un modèle de prévision numérique du temps, PNT) (lire Introduction à la prévision météorologique) permet de simuler l’évolution d’un système réel (ici, l’atmosphère). Cela produit la meilleure estimation possible du futur, appelée prévision déterministe : on utilise alors les meilleures données pour faire une unique prévision. Chacun peut constater qu’en pratique, cette prévision est souvent imprécise, à cause du manque d’observations initiales, de leurs erreurs, et des approximations effectuées lors de la simulation numérique. De plus, les erreurs de prévisions météorologiques s’amplifient fréquemment à cause du caractère chaotique de l’atmosphère : c’est l’effet papillon, par lequel une petite erreur dans les données ou le modèle peut rendre la prévision complètement fausse quelques heures ou quelques jours plus tard. Pour qu’une prévision soit utile, elle doit être meilleure qu’une prévision triviale, moins coûteuse à obtenir, par exemple un bulletin météorologique qui se bornerait à énoncer des normales saisonnières en guise de prévision. On appelle horizon de prévisibilité l’échelle de temps au-delà de laquelle on ne sait généralement pas faire de prévision utile. Cet horizon est actuellement, en moyenne, de quelques minutes pour une averse, quelques heures pour un orage, quelques jours pour une dépression ou un cyclone, quelques semaines pour une vague de froid ou de chaleur, quelques mois pour une anomalie climatique tropicale comme El Niño.

Cet horizon, et plus généralement la qualité des prévisions, sont très variables dans l’espace et dans le temps. Il est donc intéressant de connaître finement le degré de confiance que l’on peut avoir dans chacun des aspects d’une prévision : c’est l’objectif de la prévision probabiliste, où l’on produit un éventail de prévisions possibles. Comme il serait numériquement très coûteux de calculer toutes les alternatives possibles, on approxime le problème, en remplaçant le calcul d’une prévision déterministe par celui de quelques prévisions numériques perturbées aléatoirement : c’est la prévision d’ensemble. Ces prévisions sont effectuées en temps réel, comme le serait une prévision déterministe. Si l’on a n prévisions (appelées membres), l’ensemble de leurs prévisions pour un paramètre météorologique x donné (par exemple, la vitesse du vent en un point à un instant donné) est constitué de n valeurs, qui constituent mathématiquement un échantillon discret de la densité de probabilité [1] de x, compte tenu des données dont on disposait au moment de lancer la prévision. On verra en section 3 que la prévision d’ensemble produit non seulement des probabilités de paramètres, mais aussi un éventail complet de scénarios météorologiques, physiquement cohérents dans l’espace et dans le temps. C’est donc une information très riche, dont la bonne utilisation est un défi à part entière.

La notion d’horizon de prévisibilité a été popularisée en météorologie par Lorentz [2], dont l’explication des processus chaotiques en jeu par l’image de l’effet papillon a marqué le grand public. Les premières prévisions d’ensemble opérationnelles en temps réel sont dues à Toth et Kalnay [3], à l’aide du modèle météorologique américain. Depuis, la technologie de la prévision d’ensemble a été perfectionnée et appliquée dans tous les grands services météorologiques (Leutbecher et Palmer [4]), pour la prévision en elle-même, mais aussi pour l’assimilation de données. Elle s’est aussi répandue dans d’autres secteurs, comme la simulation numérique pour l’industrie, la finance, l’hydrologie, la prévision saisonnière [5] (lire La prévision saisonnière), etc.

D’un point de vue opératoire, faire une prévision d’ensemble consiste à exécuter n fois un logiciel de prévision numérique, en perturbant par des nombres aléatoires ses données d’entrées ainsi que les calculs du logiciel lui-même. Ces perturbations doivent idéalement refléter la distribution de nos incertitudes sur toutes ces données (par exemple, les erreurs d’observation) et tous ces calculs (par exemple, les processus météorologiques que l’on sait être mal modélisés, comme les flux à la surface de l’océan). Cela permet de simuler différentes évolutions possibles de toutes ces erreurs au sein du modèle de prévision et de leurs impacts sur les paramètres prévus. Les paramètres affectés par de grandes erreurs, ou par une amplification chaotique des perturbations, auront des prévisions plus dispersées que les paramètres dont la prévision reste stable malgré les perturbations : la dispersion des prévisions d’ensemble nous renseigne ainsi sur la prévisibilité des phénomènes simulés par le modèle numérique (Figure 1).

2. Comment perturber une prévision du temps ?

En pratique, on ne perturbe que certains aspects-clés des systèmes de prévision numérique, parce que notre connaissance des sources d’erreurs est très limitée. Dans l’état actuel de la technique, les perturbations portent sur :

• L’état initial de la prévision. Il s’agit d’y représenter les incertitudes du processus d’analyse, liées essentiellement aux erreurs d‘observations et aux défauts des algorithmes d’assimilation de données. La technique la plus simple consiste à ajouter à l’analyse déterministe un bruit numérique [6], par exemple gaussien, muni de corrélations spatiales et d’amplitudes fidèles aux statistiques effectuées sur des analyses passées. On peut aussi construire ce bruit par combinaisons linéaires de différences entre analyses ou prévisions récentes (méthode LAF : lagged averaged forecasting). Une méthode courante consiste à ajouter aux analyses des perturbations optimisées pour s’amplifier le plus vite possible au cours de la prévision d’ensemble. Cela permet d’être sûr que l’ensemble simulera l’effet des principales sources de chaos du jour. Une méthode plus rigoureuse, mais aussi plus chère, consiste à calculer des ensembles du processus complet d’assimilation de données(lire Assimilation des données météorologiques) : ce sont les méthodes d’assimilation d’ensemble, ou de filtre de Kalman d’ensemble.
• Les équations du modèle de prévision. Il s’agit de représenter les erreurs de modélisation. On peut pour cela mélanger dans la prévision d’ensemble plusieurs versions de modèle numérique de l’atmosphère (c’est la méthode multimodèle), ou faire varier certains paramètres-clés dont la valeur optimale est mal connue (méthode multiparamètre), voire injecter des perturbations aléatoires à certains endroits du code que l’on sait être douteux (méthode de la physique stochastique). La difficulté est que la plupart des erreurs de modélisation sont par définition inconnues, puisqu’elles proviennent de processus météorologiques qui peuvent être inconnus ; on manque donc d’information pour les simuler. Certaines sources d’erreurs ont été particulièrement étudiées, notamment la présence dans le monde réel d’échelles physiques non simulées à cause de la résolution limitée du modèle numérique ; on peut tenter de les simuler en mettant des sources d’énergie fictives dans les prévisions d’ensembles (méthode du stochastic energy backscatter, ou en français rétrodiffusion stochastique d’énergie).
• Les conditions de surface. L’interaction entre atmosphère et surfaces est une source majeure d’erreurs de prévisions. Cela provient souvent de la représentation de paramètres physiques par des valeurs artificiellement fixées au cours de la prévision météorologique, parce que l’on ne sait pas représenter correctement leur variabilité. Il faut donc représenter leurs incertitudes de manière spécifique, en les perturbant de manière cohérente avec ce que l’on sait de leur incertitude. Cela concerne en priorité les caractéristiques du sol, de la végétation, la neige, les propriétés océaniques déterminantes pour le calcul des flux de température, l’humidité et la turbulence. Dans les ensembles les plus sophistiqués, les surfaces sont elles-mêmes des modèles numériques complets dont on peut effectuer des prévisions d’ensembles couplées avec l’atmosphère. C’est notamment le cas en prévision saisonnière.
• Les couplages de grande échelle. Ceci ne concerne que les modèles numériques à domaine limité. Leurs prévisions sont sensibles aux erreurs du modèle météorologique global auquel ils sont couplés, ce qui est crucial pour prévoir l’évolution des grandes ondes atmosphériques à propagation rapide. Les prévisions d’ensemble à domaine limité doivent être couplées à des prévisions d’ensemble globales qui représentent de manière réaliste les incertitudes sur l’évolution de l’atmosphère à grande échelle.

3. De la prévision d’ensemble aux applications

La prévision d’ensemble produit une information riche et souvent difficile à comprendre. D’un point de vue mathématique, une prévision d’ensemble produit différents scénarios possibles d’évolution de l’atmosphère. Puisque la dimension de l’espace dans lequel évolue l’état atmosphérique (plusieurs milliards de degrés de liberté) est beaucoup plus grande que celle de la prévision d’ensemble (quelques dizaines de membres), cette dernière ne produit qu’un aperçu des évolutions possibles. Il existe différentes méthodes d’interprétation des prévisions d’ensemble, dont voici les principales.

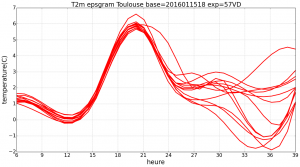
• L’examen subjectif des prévisions d’ensemble permet à un prévisionniste  entraîné (lien vers Le rôle du  prévisionniste) d’estimer la vraisemblance de différents scénarios possibles de prévision. En général il/elle va regarder un super ensemble de prévisions constitué de toutes les sorties de modèle récentes (ensemblistes ou déterministes) disponibles à l’instant où on lui demande d’interpréter la prévision. Les prévisionnistes modernes ont accès à un grand nombre de prévisions toutes vraisemblables, issues de différents centres météorologiques, de différents modèles, ou calculées à différents instants : ils/elles raisonnent toujours de manière probabiliste, qu’ils utilisent ou nom de vraies prévisions d’ensemble. La plupart des prévisionnistes privilégient le scénario consensus, c’est à dire celui qui est soutenu par la majorité des modèles et membres ; les prévisions trop atypiques sont alors rejetées car trop peu vraisemblables pour mériter d’être mentionnées dans les bulletins. Cependant, si certaines prévisions indiquent la possibilité qu’un évènement dangereux se produise, cela peut aider à lancer une alerte météorologique, au besoin en prenant le risque de lancer une fausse alerte, compte tenu de la gravité potentielle de l’évènement. Les prévisions d’ensemble peuvent être utiles pour estimer l’incertitude sur l’intensité, la localisation ou le timing des évènements météorologiques, et cela permet de les prévoir avec plus de confiance que si seules des prévisions déterministes étaient accessibles, sachant que cela nécessite un effort spécifique de la part du prévisionniste [7].

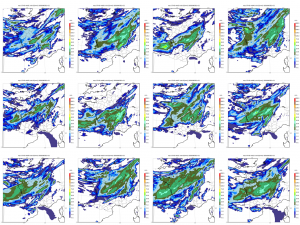
• La production de prévisions automatisées est plus performante (c’est à dire plus exacte) si elle s’appuie sur des ensembles que sur des prévisions déterministes seules, pour les mêmes raisons que ci-dessus. En effet, les ensembles apportent une information riche, qui permet de traiter les prévisions de manière sophistiquée. Ces traitements imitent souvent le travail d’expertise humaine des prévisions. Par exemple, la distribution des valeurs prévues d’un paramètre météorologique en un point de grille du modèle est une estimation de la distribution des probabilités de ce paramètre ; en chaque point on dispose d’autant de valeurs qu’il y a de membres dans l’ensemble (voir Figure 2). Ces valeurs peuvent être corrigées par des traitements statistiques destinés à compenser les défauts systématiques du modèle numérique, par exemple des biais dans les valeurs prévues, ou une trop grande confiance dans la prévision (représentée par une dispersion de l’ensemble trop faible par rapport aux erreurs constatées dans les prévisions récentes). On peut fournir aux usagers la valeur médiane prévue par l’ensemble, qui est habituellement une valeur très vraisemblable. Mais on peut faire mieux, en utilisant l’éventail des probabilités calculées par l’ensemble ; par exemple, un usager qui accepte 3 fois plus de fausses alertes d’orage que de non-détection (ce qui est, consciemment ou non, le cas de la plupart des usagers du grand public) percevra beaucoup moins d’échecs de prévision si on l’avertit du risque d’orage à partir des probabilités d’un ensemble supérieures à 25%, que si on lui fournissait la prévision médiane, ou celle d’un modèle déterministe. C’est dans les applications pour lesquelles le taux de fausses alarmes toléré est très différent de 50% que les prévisions d’ensemble permettent d’améliorer le plus les prévisions météorologiques. Cette manière d’exploiter les prévisions est semblable aux calculs d’un financier qui cherche à minimiser ses pertes en fonction des aléas du contexte économique : la prévision d’ensemble applique cette approche à des problèmes météorologiques concrets, grâce à un traitement des prévisions numériques adapté aux besoins de divers types d’usagers.
• Couplage des prévisions d’ensemble. Résumer les scénarios d’une prévision d’ensemble par des probabilités de variables météorologiques provoque souvent une perte d’information ; dans certaines applications, il vaut mieux coupler directement les sorties numériques des membres prévus aux calculs complexes spécifiques à cette application. C’est particulièrement vrai pour les applications qui sont sensibles à la distribution spatiale des variables météorologiques : la prévision des crues dépend des pluies intégrées à l’échelle des bassins versants, le routage des avions de ligne dépend du temps rencontré tout au long des trajectoires de chaque avion, la gestion du réseau électrique dépend de la cartographie des productions éoliennes et photovoltaïques et de celle du chauffage domestique, etc. Dans ces cas de figure, c’est au gestionnaire du modèle applicatif de transformer la prévision d’ensemble météorologique en une prévision d’ensemble pour ses propres paramètres d’intérêt, qui peuvent être influencés par des facteurs non  météorologiques. Cette méthode de travail s’adresse en priorité à des usagers professionnels, car ils doivent être eux-mêmes experts en utilisation des prévisions numériques météorologiques et en calculs de probabilités.

4. Que vaut une prévision d’ensemble ?

Si l’on a prévu de la pluie avec une probabilité de 50% et qu’il ne pleut pas, la prévision a-t-elle été bonne ou mauvaise ? Sur un cas isolé, il est impossible de répondre : une prévision probabiliste n’est jamais intrinsèquement bonne ni mauvaise. Pour apprécier sa qualité, il faut effectuer des statistiques sur un historique de prévisions, ce qui peut être problématique pour l’étude des phénomènes rares. Comme on l’a vu précédemment, l’utilisation même d’une prévision d’ensemble dépend de l’usager, en particulier de sa tolérance aux fausses alarmes. Pour reprendre l’exemple de la section précédente, un usager qui s’intéresse aux prévisions de probabilité d’orage de 25% (adaptée par exemple à l’organisation d’un pique-nique) aura une perception des performances d’un système de prévision très différentes de celle d’un usager qui recherche des probabilités de 80% (comme un chasseur de tornades). Ces deux facteurs (nécessité de disposer de longues statistiques, et diversité des usagers) expliquent pourquoi les mesures de qualité des prévisions d’ensemble se font avec des outils mathématiques assez complexes. En simplifiant, on peut distinguer 3 grandes catégories de mesures de qualité des prévisions qui sont pertinentes pour les prévisions d’ensembles :

• La fiabilité (en anglais : reliability) est la cohérence entre les probabilités prévues et les statistiques observées lorsqu’on compare a posteriori les prévisions aux observations. Une mesure de fiabilité basique,  la relation dispersion/erreur, est la corrélation entre (a) les variations de dispersion d’un ensemble, et (b) les variations d’amplitude des erreurs de prévision : dans un système fiable, les prévisions les plus dispersées sont en moyenne les moins bonnes, cette corrélation doit donc être la plus élevée possible. On peut aussi regarder si, lorsqu’une qu’une valeur de probabilité donnée est prévue les erreurs de prévisions constatées sont cohérentes avec cette probabilité. Exemple: sur un ensemble de cas où l’on a prévu de la pluie avec 50% de probabilité, on doit observer de la pluie dans 50% de ces cas. Les mesures de fiabilité permettent de détecter certains défauts des systèmes de prévision d’ensemble, malheureusement elles ne garantissent pas que les prévisions produites soient utiles : en effet elles ne mesurent pas à quel point les prévisions varient d’une situation à l’autre, ce qui est nécessaire pour communiquer une information adaptée à chaque situation.
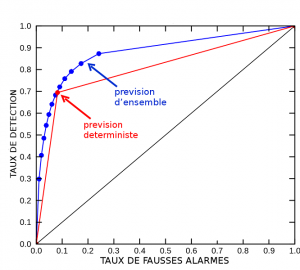
• La résolution statistique, aussi appelée acuité (resolution ou sharpness) est un type de diagnostic qui mesure à quel point les probabilités prévues sont substantiellement différentes de la climatologie (autrement dit si l’ensemble ‘prend des risques’) et quelle est alors leur justesse moyenne. L’outil le plus répandu est le diagramme ROC (receiver ou relative operating characteristic) qui mesure les taux de succès de prévisions pour tous les niveaux de probabilité prévus (c’est à dire, en moyenne sur une large gamme d’usagers possibles). Le ROC est très utile pour évaluer les performances intrinsèques d’un système de prévision d’ensemble (lien vers Le rôle du  prévisionniste) (voir Figure 3).

• La valeur décisionnelle (aussi appelée valeur économique pour des raisons historiques) mesure l’intérêt d’un système de prévision pour un type d’usager précis, dont la météo-sensibilité est souvent modélisée par (a) la valeur seuil d’un paramètre météorologique auquel il ou elle est sensible, et (b) le coût relatif qu’il/elle accorde aux fausses alarmes et aux non-détections de ce dépassement de seuil. C’est dans ce cadre que l’on peut quantifier le plus rigoureusement la valeur des prévisions d’ensemble, et en particulier ce qu’elles apportent par rapport aux prévisions déterministes [8]. Cette approche nécessite un travail spécifique de dialogue avec l’usager pour modéliser correctement sa météo-sensibilité.

Tout système de prévision doit franchir un quatrième obstacle, qui est la compréhension de l’information par les usagers. Même si les prévisions d’ensemble actuelles sont loin d’être parfaites, elles contiennent une valeur décisionnelle très élevée pour de nombreux usages. Malheureusement elles souffrent souvent d’incompréhension de la part des utilisateurs, qui leur préfèrent souvent des outils de prévision plus rudimentaires mais faciles à comprendre. Le plus grand défi actuel de la prévision d’ensemble sera la mise au point de traitement automatisés de l’information produite par les ensembles, afin de la présenter sous une forme à la fois intelligible et la plus juste possible.

 

---

Références et notes

Image de couverture : chutes de pluie prévues sur la France le 4 Août 2016 à l’aide la prévision d’ensemble.

[1] La densité de probabilité est une fonction qui décrit mathématiquement l’éventail des valeurs possibles que peut prendre un paramètre.

[2] Lorentz, E. N. 1963: Deterministic nonperiodic flow. Journal of Atmospheric Sciences. 20 : 130-141.

[3] Toth, Z., et E. Kalnay, 1993: Ensemble forecasting at NMC: The generation of perturbations. Bull. Amer. Meteor. Soc., 74, 2317-2330.

[4] Leutbecher, M., et T. N. Palmer, 2008: Ensemble forecasting. J. Comp. Phys., 227, 3515-3539.

[5] Hagedorn, R., F. J. Doblas-Reyes, et T. N. Palmer, 2005: The rationale behind the success of multi-model ensembles in seasonal forecasting–I. Basic concept. Tellus, 57A, 219-233.

[6] Les corrélations d’un bruit mesurent la relation entre sa valeur en un point, et ses valeurs aux points voisins.

[7] Novak, David R., David R. Bright, Michael J. Brennan, 2008: Operational Forecaster Uncertainty Needs and Future Roles. Wea. Forecasting, 23, 1069-1084. doi: http://dx.doi.org/10.1175/2008WAF2222142.1

[8] Par climatologie on entend la distribution statistique des situations météorologiques observées dans le passé.