Vagues et houles
PDF
Les vagues que l’on voit se propager à la surface des océans, des mers ou des lacs sont généralement dues au vent. Un corps en déplacement dans l’eau peut aussi engendrer des vagues, c’est le cas des vagues d’étrave. Le déplacement du fond de l’océan dû à un séisme ou à un éboulement sous-marin peut aussi créer une onde longue du type tsunami. Intéressons-nous plus particulièrement aux vagues dues au vent et tentons de comprendre leurs formes variées. Ceci nous amènera à utiliser certains mots du vocabulaire marin comme fetch et à comprendre aussi bien les formes variées, plus ou moins irrégulières, de leur surface que les mécanismes de leur propagation. Pourquoi certaines vagues déferlent-elles, éventuellement en formant les superbes rouleaux recherchés par les surfeurs ? Que se passe-t-il sous la surface et jusqu’à quelle profondeur l’eau est-elle agitée ? Comment évaluer et capter l’énergie de ces vagues ?
1. Des vagues aux houles régulières
La propagation d’ondes représente de façon générale la réponse d’un milieu physique à une perturbation. Une force de rappel tend alors à ramener le milieu vers l’équilibre. Dans le cas des ondes acoustiques, il s’agit de la résistance à la compression du milieu (Lire : L’émission, la propagation et la perception du son). Dans le cas d’une surface liquide, deux forces interviennent : la gravité et la tension superficielle. Cette dernière conduit à la propagation de petites rides à l’échelle du centimètre, mais les vagues et houles qui nous intéressent ici sont entièrement gouvernées par la gravité. La gravité tend localement à ramener la surface libre vers sa forme d’équilibre horizontale, mais ce mouvement induit des forces de pression qui transmettent le mouvement à l’eau environnante, et propagent ainsi la perturbation.
Les vagues sont produites par le vent selon des mécanismes complexes qui font encore l’objet de recherches. Cependant lorsqu’elles s’éloignent de leur zone de génération, les vagues se régularisent et on parle alors plutôt de houle. Cette houle peut être décrite comme une somme d’ondes sinusoïdales élémentaires qui se prêtent bien à l’analyse mathématique.
Figure 1. Canal à houle et son batteur [Source : © LEGI]
De telles houles régulières sont reproduites dans des bassins par des batteurs mécaniques oscillants (Figure 1). On peut alors fixer les paramètres qui contrôlent leur comportement : leur période et leur amplitude, ainsi que la hauteur d’eau du bassin.
2. La houle de faible amplitude
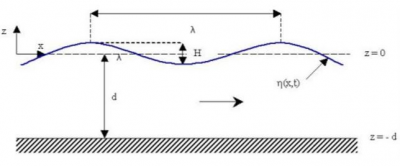
Dans cette limite de faible amplitude, les équations de la mécanique des fluides admettent des solutions simples, de forme sinusoïdale. On parle alors de houle d’Airy, du nom du mathématicien et astronome britannique George Biddell Airy (1801-1892).
Outre son amplitude, cette houle est caractérisée par sa période T (la durée d’une oscillation en un point donné) et sa longueur d’onde λ (la distance entre deux crêtes successives). La longueur d’onde est reliée à la période par la vitesse de propagation c=λ/T, qui dépend de la hauteur d’eau selon une formule donnée par la solution mathématique.
![]() où g représente l’accélération de la pesanteur. Une houle de longueur d’onde λ=10 m se propage ainsi à la vitesse c=4 m/s, et une houle de longueur d’onde λ=100 m se propage plus rapidement, à vitesse c=12,5 m/s. Les périodes correspondantes, T=λ/c, sont respectivement T=2,5 s et T=8 s. En combinant ces formules on peut aussi exprimer la longueur d’onde comme λ=gT2/ (2π).
où g représente l’accélération de la pesanteur. Une houle de longueur d’onde λ=10 m se propage ainsi à la vitesse c=4 m/s, et une houle de longueur d’onde λ=100 m se propage plus rapidement, à vitesse c=12,5 m/s. Les périodes correspondantes, T=λ/c, sont respectivement T=2,5 s et T=8 s. En combinant ces formules on peut aussi exprimer la longueur d’onde comme λ=gT2/ (2π).
L’autre cas limite correspond à l’eau peu profonde, pour laquelle la longueur d’onde est grande par rapport à la profondeur d. Dans ce cas l’onde se propage à la vitesse ![]() , indépendante de la longueur d’onde. Par exemple un tsunami se propage avec une longueur caractéristique de l’ordre de la centaine de km, grande par rapport à la profondeur océanique, de quelques km. On est alors dans le régime d’eau peu profonde, et pour d=4 000 m, la vitesse de propagation c=200 m/s. La marée se propage également à la surface de la Terre comme une onde d’eau peu profonde, avec une période principale de 12 h, et une longueur d’onde correspondante de plusieurs milliers de km (Lire : Les marées).
, indépendante de la longueur d’onde. Par exemple un tsunami se propage avec une longueur caractéristique de l’ordre de la centaine de km, grande par rapport à la profondeur océanique, de quelques km. On est alors dans le régime d’eau peu profonde, et pour d=4 000 m, la vitesse de propagation c=200 m/s. La marée se propage également à la surface de la Terre comme une onde d’eau peu profonde, avec une période principale de 12 h, et une longueur d’onde correspondante de plusieurs milliers de km (Lire : Les marées).
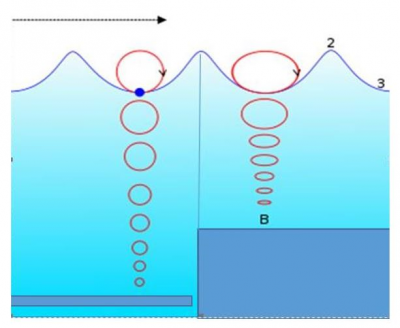
Il ne faut pas confondre la vitesse de propagation de l’onde avec la vitesse de déplacement des particules d’eau, celle-ci est beaucoup plus faible et donne pour les particules une trajectoire circulaire en eau profonde (voir Figure 3). Pour les particules situées à la surface libre le diamètre de la trajectoire est égal à la hauteur totale H de la houle. La vitesse du fluide est donc égale à πH/T, nettement plus petite que la vitesse de propagation λ/T pour une houle sinusoïdale. Le diamètre de ces trajectoires tend exponentiellement vers 0 avec la profondeur, devenant pratiquement nul à une profondeur égale à une demi-longueur d’onde.
En eau peu profonde ces trajectoires deviennent elliptiques et s’aplatissent vers le fond, la composante horizontale ayant une grande importance pour le transport sédimentaire.
Ces trajectoires sont fermées, et le déplacement moyen d’une particule fluide est donc nul. Cependant il ne s’agit que d’une première approximation, valable seulement dans la limite d’une onde de très faible amplitude. Les particules se déplacent en réalité d’une distance de l’ordre de 40H2/λ par période. C’est ce qu’on appelle la dérive de Stokes, nommé d’après le mathématicien britannique George Gabriel Stokes (1819 -1903) qui l’a décrite et calculée. Pour une houle de hauteur H=2m et de longueur d’onde λ=100 m le déplacement est ainsi de 1,6 m par période.
3. Les houles non-linéaires
La houle sinusoïdale n’est qu’une première approximation valable pour les faibles amplitudes. On parle alors de « houles linéaires » correspondant à la forme simplifiée des équations du mouvement, dite « linéaire ». Dans cette approximation tout champ d’ondes peut être décrit comme une addition d’ondes élémentaires sinusoïdales, chacune gardant son identité.
En dehors des houles linéaires d’Airy on peut distinguer deux types de houles non- linaires :
– les houles de plus grandes amplitudes en eau profonde
– les houles en eau peu profonde
3.1. Houle en eau profonde
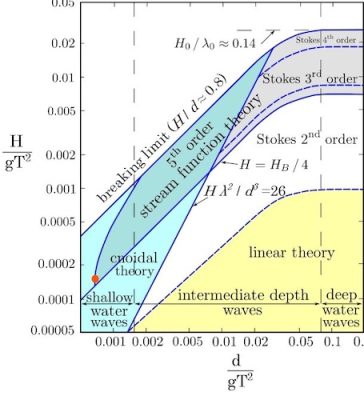
La droite du graphique de la figure 4 correspond à l’eau profonde, pour laquelle des solutions mathématiques périodiques plus complexes ont été obtenues par le mathématicien George Gabriel Stokes déjà mentionné. Les ondes de Stokes du 2e, 3e, ou 4e ordre correspondent à des amplitudes croissantes, qui nous éloignent de plus en plus du cas sinusoïdal : les creux deviennent de plus en plus étalés, et les crêtes de plus en plus aigües, jusqu’à former un sommet anguleux (d’angle 120°). A ce stade l’onde devient instable et se brise par déferlement. Sa courbure représentée par le rapport H/l atteint une valeur limite de l’ordre de 0.14, et au-delà de cette amplitude limite, il n’existe plus de houle périodique : elle déferle.
3.2. Houle en eau peu profonde
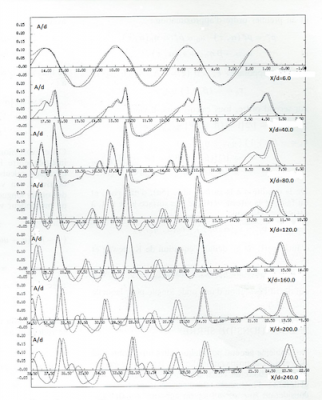
La Figure 5 (en trait plein) montre l’évolution d’une houle initialement sinusoïdale se propageant dans un canal à houle à fond horizontal. La hauteur d’eau est de d=10 cm, tandis que la hauteur de la houle initiale est H=2,5 cm et sa période T=4 secondes, ce qui donne une longueur d’onde de 4 mètres. La profondeur relative d/gT2 est donc égale à 0.0006 et la hauteur relative H/gT2 à 0.00015, ce qui est représenté par le point rouge sur la Figure 4. Ceci nous situe bien dans le domaine de l’eau peu profonde.
Chaque courbe en trait plein donne l’évolution temporelle de la dénivellation à différentes distances relatives x/d de l’origine où l’onde est produite par un batteur oscillant (comme celui représenté sur la Figure 1). Rapidement chaque période initiale se décompose en une suite de pics d’amplitude décroissante et de célérité décroissante. Ainsi le pic principal de chaque période peut rattraper les pics secondaires de la période précédente.
Les théories de Stockes, même aux ordres supérieurs, donnent une mauvaise représentation de ces phénomènes. Une meilleure représentation mathématique de la propagation des ondes en eau peu profonde fait appel à des équations non linéaires (équations K D V) qui portent le nom des scientifiques qui les ont étudiées : Korteweg (1848-1941) et De-Vries. Sur la Figure 5 une simulation numérique (en trait pointillé) de la propagation de la houle à l’aide de ces équations est en très bonne coïncidence avec les enregistrements.
4. Houle cnoïdale et ondes solitaires
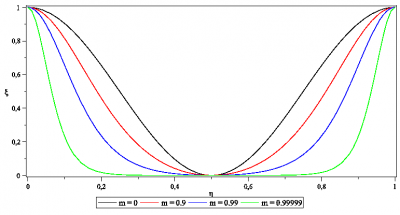
Les ondes solitaires ont la propriété remarquable de se former spontanément à partir de conditions initiales plus douces comme on l’a vu sur la Figure 5. Dans la nature c’est le cas d’un tremblement de terre en zone maritime qui génère au large une vague de tsunami de l’ordre du mètre. Celle-ci s’amplifie quand la profondeur d’eau au voisinage des côtes diminue et se décompose en un train d’ondes solitaires dont l’amplitude peut atteindre une vingtaine de mètres. De telles vagues deviennent alors dévastatrices et mortelles comme ce fut le cas au Japon avec 23 500 morts (2015) et en Indonésie avec plus de 200 000 morts (2004). (Lire : Tsunamis, les connaître pour mieux les prévoir)
5. Raidissement de la houle à l’approche d’une plage

La houle est aussi déviée par un changement de profondeur, à cause du phénomène de réfraction. Ainsi à l’approche d’une plage, les lignes de crête ont tendance à suivre les lignes bathymétriques [2], comme on le voit sur la Figure 7. Cet effet est dû à la diminution de la célérité de la houle à plus faible profondeur. De façon analogue la lumière est déviée en entrant dans un milieu à fort indice de réfraction, où elle se propage moins vite.
La houle se raidit aussi de plus en plus à l’approche de la plage, jusqu’au déferlement. Cet effet est dû à la diminution de la célérité de propagation à flux d’énergie constant, ce qui implique une augmentation de la densité d’énergie, et donc de la hauteur de vague, ainsi qu’une diminution de la longueur d’onde. A faible profondeur, la crête de l’onde se propage plus vite que les creux ce qui conduit au déferlement final.

Il peut arriver que des trains de houles arrivent de directions différentes et par interaction donnent des houles croisées ou un état de mer dit « gaufré ». La Figure 8 représente une mer gaufrée en eau peu profonde où les houles relativement régulières présentent un profil de type cnoïdal avec un creux plus allongé que la crête ; une légère réflexion au voisinage de la côte apparait.
Enfin, la houle est influencée par la morphologie côtière, mais sculpte aussi en retour le rivage à long terme, par l’érosion des côtes rocheuses et des plages, ainsi que par le dépôt de sédiments au gré des courants qu’elle induit.
6. Houles de mer et génération par le vent
Le vent qui souffle à la surface de la mer transfère une partie de l’énergie de l’atmosphère vers la surface de l’eau. C’est un phénomène de frottement des couches d’air sur l’eau qui crée des dépressions sur les crêtes et des surpressions dans les creux, ayant pour effet d’amplifier des vaguelettes initiales pour former un régime complexe de vagues de plus en plus longues et puissantes au fur et à mesure de leur propagation.
En eau profonde les paramètres mis en jeu sont la vitesse du vent, la longueur de la zone où souffle le vent appelée fetch et la durée pendant laquelle souffle ce vent. La profondeur d’eau aura aussi une influence si celle-ci est faible. Par exemple un vent qui souffle à 15 m/s pendant 10 heures sur un fetch de l’ordre de 100 km engendre des vagues de hauteur significative Hs (voir définition ci-dessous) de l’ordre de 3 m. Notons que la vitesse du vent croît avec la hauteur : la vitesse de référence, notée U10, est celle mesurée à 10 mètres au-dessus de la mer (en position moyenne).
7. Houles irrégulières
Il y a deux façons de les analyser : l’analyse statistique locale et l’analyse spectrale.
7.1. Analyse statistique locale
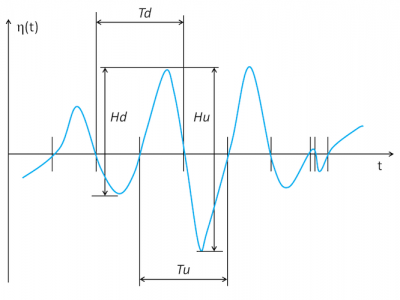
– la hauteur d’un creux à la crête suivante est dite downcrossing et notée Hd ;
– d’une crête au creux suivant c’est la hauteur upcrossing notée Hu.
Les valeurs moyennes de Hd et de Hu sont les mêmes et donnent une estimation de la hauteur total H. On fait de même pour la période avec Td et Tu pour avoir une estimation de la période T.
Dans la pratique, on s’intéresse plutôt à ce que l’on appelle la hauteur significative Hs qui correspond à la valeur moyenne des hauteurs du tiers des vagues les plus hautes [3]. La météo marine donne Hs qui est calculé par modélisation numérique à partir du spectre de la houle, connaissant la vitesse du vent et le fetch (voir 7.2). Dans les zones côtières peu profondes le modèle intègre aussi la topographie du fond.
7.2. Analyse spectrale
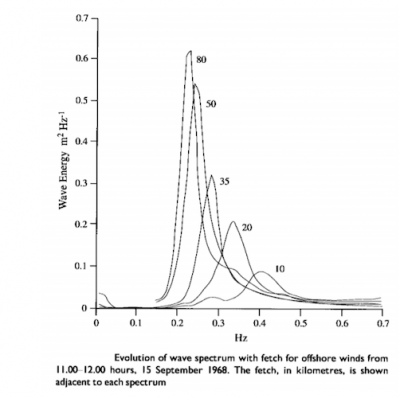
7.3. Vague scélérate
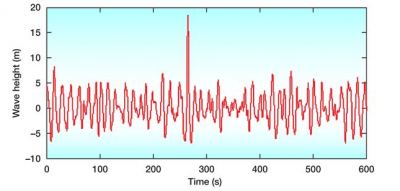
Il arrive parfois qu’une vague de très grande amplitude (deux à trois fois Hs), nommée vague scélérate, apparaisse au milieu d’un train de vagues. Les récits de ce phénomène observé par différents marins ont longtemps été mis en doute. Cependant les méthodes modernes d’enregistrement ont permis de confirmer cette réalité. Sur la Figure 9 apparait le signal d’une vague scélérate dont la hauteur est de l’ordre de 26 mètres parmi un train de vagues d’amplitude significative Hs de 11,8 mètres. Cet enregistrement a été réalisé le 01/01/1995 sur la plateforme pétrolière Draupner au large de la Norvège. Une vague est qualifiée de scélérate quand elle apparait de façon isolée au milieu d’un train de vagues avec une amplitude de plus de 2 fois supérieure à l’amplitude significatrice de ce train. On estime que 22 cargos ont coulé entre 1973 et 1994 à cause de vagues scélérates, faisant des centaines de victimes [5].
L’origine d’une vague scélérate n’est pas encore bien comprise et pourrait être expliquée par des interactions non linéaires ou par rencontre de trains de vagues d’origines différentes. Cependant des scientifiques ont pu réaliser en laboratoire une expérience qui met en évidence une vague scélérate issue du croissement de deux trains de houles croisées faisant un angle de 120 degrés [6].
8. Energie houlomotrice
L’énergie cédée par le vent à la houle est-elle récupérable? C’est une question qui a pris toute son importance ces dernières années dans le cadre de la recherche des énergies renouvelables. Une formule d’approximation permet de chiffrer la puissance E (énergie apportée par seconde) par mètre linéaire de crête, E=0.5Hs2.T (kW/m). Environ 2% des 800 000 km de côtes mondiales ont une puissance énergétique moyenne supérieure à 30 kW/m, ce qui correspond à une puissance totale de l’ordre de 0.5 TW [7], soit une production annuelle d’énergie électrique d’environ 2 000 TWh (8% de la consommation mondiale) [8].
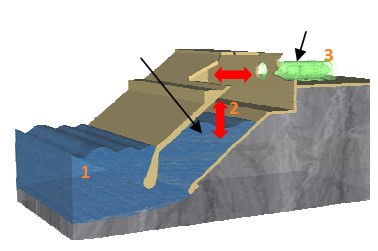

of the Basque Government (EVE)]
Un prototype pré-commercial a été construit à Mutriku dans le golfe de Gascogne par l’agence basque de l’énergie et mis en service en 2011. Cette centrale houlomotrice de puissance 300 kW est incorporée dans un brise-lame (Figure 13).
9. Message à retenir
- Les vagues sont générées par le vent dans la zone de fetch ;
- En dehors de la zone de fetch, les vagues se lissent pour donner des houles plus ou moins régulières ;
- Au voisinage du littoral, les houles se déforment sous l’influence des variations de bathymétrie et de morphologie de la côte ;
- Dans les zones littorales, en combinaison avec les courants les houles ont une importance fondamentale sur le transport sédimentaire ;
- L’énergie des vagues peut être en partie récupérée.
Notes et références
Image de couverture. [Source : VIGNA christian, CC BY-SA 4.0, via Wikimedia Commons]
[1] Ces solutions font intervenir les fonctions elliptiques de Jacobi notées cn, d’où l’adjectif « cn-oïdal ».
[2] Lignes d’égale profondeur, équivalentes aux lignes de niveau pour les reliefs (du grec ancien bathys signifiant « profond »)
[3] Cette hauteur Hs donnée par les bulletins météo est environ 4 fois l’écart type de la déviation verticale de surface η (l’écart type est la racine carré de la moyenne de η2). La relation précise entre ces deux quantités est cependant complexe et dépend des conditions de vent.
[4] Hasselmann et al. (1973) Measurements of wind-wave growth and swell decay during the Joint North Sea Wave Project (JONSWAP), Ergnzungsheft zur Deutschen Hydrographischen Zeitschrift Reihe, A(8) (Nr. 12), p.95.
[5] https://fr.wikipedia.org/wiki/Vague_sc%C3%A9l%C3%A9rate
[6] Allister et al. (2019) Laboratory recreation of the Draupner wave and the role of breaking in crossing seas, J. Fluid Mechanics 860, 767-786.
[7] Le terawatt (TW) est une unité de puissance qui correspond à 1012 watts soit un milliard de kilowatts. Un TWh est l’énergie totale apportée par 1 TW pendant une heure (soit 3600 terajoules).
[8] www.irena.org/Publications/2014/wave-énergie
L’Encyclopédie de l’environnement est publiée par l’Association des Encyclopédies de l’Environnement et de l’Énergie (www.a3e.fr), contractuellement liée à l’université Grenoble Alpes et à Grenoble INP, et parrainée par l’Académie des sciences.
Pour citer cet article : TEMPERVILLE André (2 novembre 2021), Vagues et houles, Encyclopédie de l’Environnement. Consulté le 21 décembre 2024 [en ligne ISSN 2555-0950] url : https://www.encyclopedie-environnement.org/eau/vagues-houles/.
Les articles de l’Encyclopédie de l'environnement sont mis à disposition selon les termes de la licence Creative Commons BY-NC-SA qui autorise la reproduction sous réserve de : citer la source, ne pas en faire une utilisation commerciale, partager des conditions initiales à l’identique, reproduire à chaque réutilisation ou distribution la mention de cette licence Creative Commons BY-NC-SA.







