声音的产生、传播和感知

轻柔的乐符、发动机的嗡鸣、电钻的尖响……这些声音是如何产生,又是如何传到我们耳中的呢?声音由在可压缩介质(特别是液体和固体)中传播的振动组成。在不同的介质中,声音的特性也各有不同。本文不仅讨论频率、波长和声强的概念,还会以秋千和小提琴的乐音为例,来进一步说明模态和共振的概念。
1. 声音究竟是什么?

声音又名声波(acoustic waves),是一种疏密相间的波,能够通过空气或任何其他可压缩的介质,从声源传播到接收者;声源通常为受到机械激励的具有一定弹性的固体材料,如:一块受到锤子敲击而振动的铁砧,一根被音乐家手指拨动的吉他琴弦,或一片因电磁铁作用而鼓动的扬声器膜片。同样地,空气或水等流体在受到扰动(如螺旋桨、喷嘴喷出的气流、车辆运动产生的湍流等)而出现压力波动时,也会发出声音,并在环境中传播。
流体中的分子可以向周围传递自身振动,带动相邻的分子层随之运动,这些分子层又将这种疏密相间的振动继续传递给下一分子层,如此循环(如封面动画所示)。众所周知,空气看似静止,却包含大量不断无规则运动的分子,且可以压缩[1]。空气对改变其分子层密度和位置的振动非常敏感,因而能够传播声波。水同样由无规则运动的分子组成,但密度要比空气大得多(约为空气的800倍),而可压缩性则弱得多(约为空气的1/100000),分子之间存在着难以克服的库仑斥力[2]。水和其他液体也具备传导声音的能力。
[图片来源:DR]
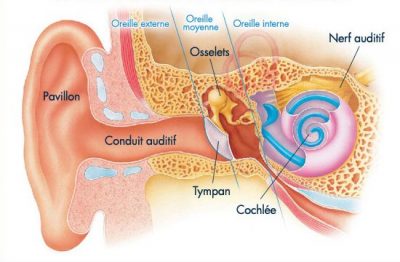
(图2.Oreille externe 外耳,Oreille moyenne 中耳,Oreille interne 内耳,Pavillon 耳廓,Conduit auditif 耳道,Osselets 听小骨,Nerf auditif 听觉神经,Tympan 鼓膜,Cochlée 耳蜗)
当分子间的压力变化传播到接收器,通常是鼓膜(图1)或麦克风膜片等柔性膜时,接收器将随最近的分子层一同振动。对于人耳或动物耳(图2)而言,听觉神经会将接收到的信息传递给大脑,进行识别和解读;而对于麦克风而言,膜片的振动将被转换为电信号记录下来,或由音频扬声器放大后重新传输。
2. 速度、频率和波长
在空气等气体中,声音的传播得益于一大基本性质:分子的运动性。在标准状态下,分子运动的平均速度约为480 m/s(详见《压强、温度和热量》)。但是这种运动并不是定向的,而是向四面八方扩散能量。然而,声音在空气中的传播速度,或者说波速(celerity),反映的则是一个极小体积内的所有分子(即一个流体质点)在同一方向上的集体有序位移。这就解释了为什么声速虽然与分子的平均速度有关,但却只能达到该平均速度的一个分数,约为340 m/s。
真空中的光速约为300000 km/s,空气中的光速与之相差无几。相比之下,声速就缓慢得多。正因如此,在足球比赛中,坐在距离中圈约170米的看台上的观众,在看到球员的脚触球半秒钟后,才能听到踢球的声音。尽管如此,但在相对较短的距离内,如音乐厅一类的小空间,声波就能够原原本本、近乎同步地将乐符信息传递到乐迷耳中供其欣赏。关于声速与光速,有一道经典的练习题:在暴风雨中,我们几乎是瞬间就能看到闪电,那么该如何估算出风暴距离我们有多远呢?

周期(period)T是所有波的主要性质之一;对于声波而言,T是以给定时间点为始,两个相邻密部或疏部的间隔时间。相比之下,周期的倒数即频率(frequency)f(f = 1/T)更为常见,且可与周期起到相同的描述效果。频率表示每秒钟振动的次数,单位为赫兹(Hz,1 Hz = 1s-1)。在声速c和周期T或频率f已知的情况下,可以很容易地计算出声音的振动波长(wavelength of sound vibration)λ = cT = c/f,即两个相邻密部或疏部之间的距离。1000 Hz的频率刚好位于可听声波的频段中点,而与该频率相对应的波长为34 cm(见图3及后文段落)。
在我们所处的环境中,一切物体都处于运动当中,也因此会不可避免地发出声音。在我们体内,血液在循环,肺部在扩张与收缩,消化系统也在持续运转,但我们相对柔软的肉体可以很好地吸收这些压力变化,因此,医生需要用听诊器才能听到我们的心跳或支气管内气流的速度变化。此外,人耳只对15 Hz到15000 Hz这段相对较窄的频谱内的声音敏感。因此,除了自己的嗓音,我们感知不到体内的其他响声,这也使得我们能够将注意力更好地集中在外界的声音上,这些声音通常更悦耳,最重要的是,它们能让我们捕捉到更为有用的信息。不同种类的动物能感知到的声音频段也大相径庭。例如,大象能够发出并听到低于10 Hz的次声波,彼此之间也用该频段的声波进行交流。与之相反,蝙蝠却能发出并听到频率超过30000 Hz的超声波,这些超声波在周围环境中反射产生回声,帮助它们探测完全黑暗的环境。
通常来讲,声速与频率无关,但取决于介质密度,因而对温度和压力的变化非常敏感。介质的密度越小、可压缩性越弱,声速就越大。所以,在可压缩性接近空气、但密度却比空气低得多的氦气中,声速约为其在空气中的3倍。
3. 声音的强度
我们一般用声压(sound pressure)p来表示声音的强度,这一物理量指的是声波造成大气压力局部波动的最大振幅。通常来说,这种波动是非常微弱的。例如,一个正常说话的人会在一米外产生约0.01帕斯卡(Pa)的声压,是正常大气压(约为105 Pa)的千万分之一。
声压与图2所示的最大振幅成正比;而相较于声压本身,人耳听觉实际感知到的声音强度显然更与其对数[3]成正比关系。这意味着当声压高出10倍,人耳感受到的声音强度是原来的2倍;声压高出100倍,则人耳感受到的强度是原来的4倍。声波的强度与声压的平方成正比,故取10 log10(p2/p2ref)=20 log10(p/pref)来表征声音的强度,并称之为分贝。分贝(dB)或1/10贝尔是常用的声强单位,是为了纪念发明电话的苏格兰科学家格雷厄姆·贝尔(Graham Bell,1847-1922)而命名的。它等于20 log10(p/pref),其中p表示声压,pref为参考压力,随机设定为20 μPa(20×10-6帕斯卡,或十亿分之零点二个标准大气压),这一参考值能够代表大多数人的最低听力阈值[4],即0 dB。因此,声音强度每增加20分贝,则表示声压或声音振幅扩大了10倍,或声音的强度(又称声强,sound intensity)扩大了100倍。
以下给出了一些情况下的声音强度数值,它们赋予分贝实际意义:
- 宁静的乡村:40 dB或p=2×10-8个标准大气压。
- 车水马龙的繁华街道:80 dB或p=2×10-6个标准大气压。
- 飞机起飞时的机场:120 dB或p=2×10-4个标准大气压。
- 短时间内暴露的法定安全限值:135 dB或1/1000个标准大气压。
众所周知,当呼喊一个正在走远的人时,我们需要不断地提高嗓门。任何声源发出的声音在传播过程中,其强度都会迅速降低,原因有二:第一,声波离开声源后,其能量会呈半球面状不断扩散,因此,随着半球面积的增加,声波强度也逐渐降低,这一趋势可用与声源距离平方的倒数来表示。第二,这种由气体压缩和膨胀而形成的初始能量,会经由粘性耗散转化为热量(详见《压强、温度和热量》)。
4. 简谐运动:摆锤和秋千

让我们以单摆为例,开启对振动现象的探索与发现。单摆只有一个自由度[即用于表示物体在运动轨迹上的位置或重心的参数或坐标],重心始终保持在一段弧形的轨迹上(图4)。当外力刺激刚刚停止,起始扰动结束的情况下,摆锤将以一个明确的频率继续摆动,该频率被称为固有频率(natural frequency)。在小幅摆动的情况下,固有频率等于(1/2π)(l/g)1/2,其中l表示单摆的长度,g表示重力加速度。固有频率取决于重力,这一事实反映了势能(高点处的最大值)和动能(低点处的最大值)之间的转换。上述这种有规律的周期性运动正是摆锤的振动模式。
现在,假设我们以给定的频率为摆锤增加额外的能量。例如,每当摆锤通过最低点时,都推动它一次,来提升其速度;这一额外的能量将与摆锤先前的能量累加,使摆锤的振幅增大。我们称这种推动与摆锤的振动同相(in phase),并且引发了摆锤的共振(resonance)。共振会增大振幅,每次推动增加的能量都刚好可以与振动过程中耗散的能量相抵。相反地,如果系统得不到能量供给,每振动一次,摩擦力就会耗损一部分能量,振幅也因此会逐渐减小。

[来源:《少女心中的爱情升华》,弗拉戈纳尔(Fragonard)的布面油画]
秋千的例子(图5)展现了另一种形式的共振。孩子们稍加练习就能加速冲向最低点,从而增加摆动的幅度。此外,值得注意的是,当秋千经过最低点时,他们会尽可能地沿着运动轨迹切线方向平躺,从而减少空气阻力,同时提供额外的能量。
5. 驻波:弦振动与音乐
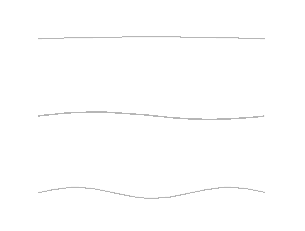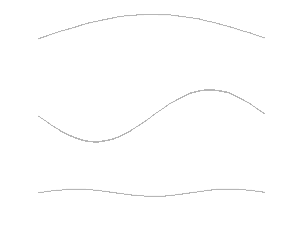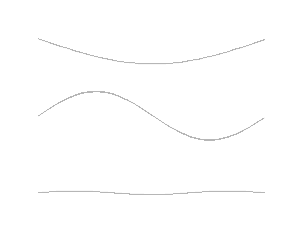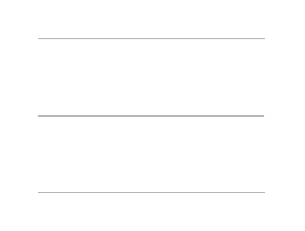
摆锤和秋千都不会发出声音(安全扣的吱吱声除外)。因此,除了上述的简单案例,我们也有必要借助新例子,进一步说明振动的物体是如何发出声音的。这种发声系统的原型是一根在两个定点之间拉紧的弦,在受到激励后开始振动,同时发出声音。这便是用小提琴、吉他、竖琴或其他弦乐器演奏乐曲的过程。这种机械系统非常复杂,因为在弦上存在无数个分布于任意位置的自由度,以及许多不同的模态。我们将其分波长是两定点间距两倍的基波(fundamental mode),和频率为基波整数倍的谐波(harmonics)。图6中的动画展示了最简单的三种模态,由此我们可以推测出无限多的可能的谐波。
[来源:克里斯托夫·当国·陈(Christophe Dang Ngoc Chan,cdang)(个人作品)[美国国家地球物理流体动力学实验室(GFDL),http://www.gnu.org/copyleft/fdl.html或知识共享许可协议(CC-BY-SA-3.0),http://creativecommons.org/licenses/by-sa/3.0/],维基百科共享资源]
这种振动系统最有趣的特性之一是其能够形成驻波(standing waves),如图6的动画所示。驻波的鲜明特点在于它是由一系列的波节(knots),即振幅为零的点,和波腹(bellies),即最大振幅所在的点组成的。波节和波腹的数量取决于两个固定点之间的距离和弦的张力。弦上的波似乎停在原地,并未沿着某一方向传播,这一现象正是驻波这一名字的由来。这种非常特殊的波也能够在周围空气中传播,不断地将弦发出的声音传递到听众的耳朵或麦克风中。音符的时长则取决于施加的激励(如,用琴弓摩擦小提琴琴弦)的时长。
此外,在固定端和自由端之间也可以产生驻波。但这种驻波的基波只包含1/4波长。音叉就是这一现象的最佳写照,它由两根金属棒而非振动的弦组成,却能够发出音准极高的“A”(音名,对应唱名La,译者注),可作为整个管弦乐队的参考音。
通常,弦的振动可闻却不可见,但下面视频中的驻波火焰管却是一个特例。沿管道分布的一系列小孔处可以显示管中丙烷气压的周期性波动。无论是通过小孔的气体流量,还是每个小火焰的高度,都与该处的压力成正比,在波节处为零,在波腹处最大。
在所有乐器,尤其是弦乐器中,声音的产生源自物理激励带来的振动与一组特定模态(包括谐波)之间的共振(如图6与上文视频所示)。音乐家正是通过找寻这种共振,来选择自己想要演奏的音符。所发出声音的音准取决于对激励方式的精确选择。一般来说,单根弦的振动几乎是听不到的。这就解释了为什么小提琴、大提琴和吉他的琴弦要与共鸣板(soundboard)相连,二者与其他部件又共同组成共鸣箱(sound box)(图7)。共鸣箱本身具有振动波,可以与琴弦的振动形成共振。
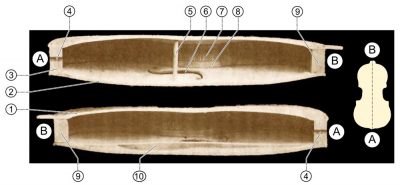
[图片来源:英语:未知照片。由德克(Dake)改进和(略微)补色。编号由SuperManu添加;法语:原始摄影师未知。由德克(Dake)改进和(略微)补色。编号由SuperManu添加。(路德艺术(奥古斯特·托尔贝克(Auguste Tolbecque)))
[来源:美国国家地球物理流体动力学实验室,GFDL(http://www.gnu.org/copyleft/fdl.html),知识共享许可协议(CC-BY-SA-3.0,http://creativecommons.org/licenses/by-sa/3.0/,CC BY-SA 2.5-2.0-1.0,http://creativecommons.org/licenses/by-sa/2.5-2.0-1.0),维基百科共享资源]
得益于其尺寸,共鸣板可以将声音放大并传播到空气中,进而传播给听众。最后,需要说明的是,共鸣板的面积决定了乐音的音域[5]。从500 cm2的成人小提琴(图7中AB点之间的长度约为35-36 cm)到1000 cm2的大提琴,再到2000 cm2的低音提琴,不同音域的乐器共同组成了交响乐团。
悬崖峭壁、古剧院的围墙、隔音屏障……众所周知,天然或人造的壁面会对感知到的声音信号产生显著影响。这种影响是由两个因素共同决定的:一是其形状是否利于共振,二是其表面条件。光滑、坚固、富有弹性的壁面能很好地反射声音;相反地,粗糙或者涂有柔性吸波材料的墙壁则不利于声音的反射,这与回声(echo)现象有关。目前,对回声现象的研究已有诸多重要的应用,如设计高音质音乐厅,减轻噪声污染等。
6. 声音在水和固体中的传播
因为声音的产生源自介质的可压缩性,所以所有的介质都可以传导声音,特别是水等液体。人们对声音在海洋中的传播尤其感兴趣,因为光不能穿透很深的海域,这种情况下,声音就成为了首选方案之一。渔民探测鱼群,地理学家考察水下的地形地貌,世界各国海军识别附近敌友舰艇,都离不开声波或超声波。海洋中的哺乳动物也是通过超声波来进行交流的。在海水中可以使用的音频范围从30 Hz到1.5 MHz,这个值比15000 Hz的人类听觉极限高出约100倍。水中的声速约为1450至1550 m/s,如图8所示,它主要随温度和深度(即压力)变化而变化,但对盐度变化并不敏感(见《海洋环境》)。
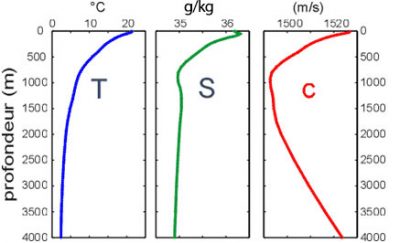
[来源:http://lecalve.univ-tln.fr/oceano/fiches/fiche3F.htm]
在海洋中,声波会在海水表面发生反射,因此在水上是无法直接听见水下的噪声的,需要使用声纳(sonar)这种特殊装备进行采集。此外,在海底、海洋中的分层处,如温跃层(见《海洋环境》),以及不同密度水体的交汇处,特别是主要的河流入海口附近,声波也会发生反射。即使没有穿过清晰的分层,声音的路径也很少是一条直线。声波通常会向声速较低的区域转折并聚集,并在该区域内发生波导(waveguide)作用[6]。对于海洋表层和声速最低的中间层(图8中约1000 m处)而言,这一现象尤为明显。1000 m以下的各层因此形成了“声音盲区”,只有将发射和接收系统置于这一深度以下才能对其进行探测。
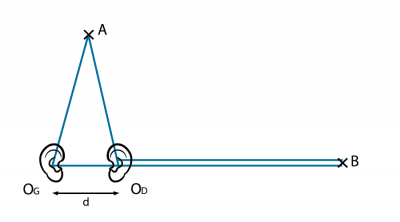
人体主要是由水组成的,因而不能在水下反射声波。由于双耳之间存在一定距离(约17cm),人类在空气中可以感知到两种不同的声音,而它们的相移(phase shift)使得追溯声源成为可能。前文提到,频率为1000 Hz的声音,其波长等于34 cm。如果声源位于听者前方(图9中的点A),且与左右耳的距离相等,那么两只耳朵会同时感知到这个声音,而不存在任何相移。但如果声源位于两耳的连线上(图9中的B点),耳朵感知到的声音会产生一个d/c为1/2000 s的时移,d/λ值为17/34,即波长的一半[7]。这种显著的相移能够使大脑感知到声源方向。指挥家可以根据相移识别出合奏中每种乐器发出的声音。
相比之下,在水中,当声源位于侧面,即相移最大时,人耳感知到的声音时移(d/c)约为1/10000 s。当频率为1000 Hz时,d的值仅相当于波长的十分之一,无法被人耳察觉。因此,人类在水下无法辨别声源。然而,对海豚等海洋哺乳动物来说,其发出的声音比人耳能感知到的最高频率还要高10到100倍,波长(λ)一般在1.5-15 cm之间,小于它们两耳之间的距离(约15 cm)。因此,即使声源与它们的耳朵不在一条直线上,与波长相比,这些声音的相移也已经足够显著,不仅能让它们相互交流,还能让它们在黑暗的海底定位彼此或可能的障碍物。
在固体介质中,声音的传播速度甚至比在液体中还要快。这是因为固体比液体的可压缩性更弱。在本文开头提到的铁砧中,声音的传播速度约为5000 m/s,如果其长度约为50 cm,则意味着整个铁砧仅在1/10000 s内就能感受到锤子的冲击,而空气中的声波需要几乎2 ms才能传播相同的距离。换言之,铁匠听到的打铁声,是整个铁砧,而不仅仅是被锤子敲击的区域发出的。
参考资料及说明
封面图片:由径向振动的球体发出的声波,通过相邻气体层疏密相间的振动,向四面八方传播。[来源:蒂埃里·杜格诺尔(Thierry Dugnolle)(个人作品)[CC0],维基百科共享资源]
[1] 空气的可压缩性既大到足以使这种流体介质传导声音,又小到可以在远低于声速的速度下用不可压缩的流体力学方程来近似描述空气动力学。
[2] 构成水分子的氢原子和氧原子的原子核周围,带负电荷的电子受到库仑力的作用,在距离非常小时,彼此之间会发生强烈排斥。这种排斥力也会影响原子和分子。
[3] 对数是一种数学运算,两个数乘积的对数等于这两个数各自的对数之和:log (ab) =log(a)+log(b)。例如,声压增加10倍,则其以10为底的对数只增加1倍。在通常的记法中,log10 指的是以10为底的对数,而Log指的是以e为底的纳皮尔(Naperian)对数,其底数为无理数e = 2.71828…
[4] 分贝(dB)是以苏格兰科学家、电话的发明者格雷厄姆贝尔(Graham Bell,1847-1922)的名字命名的。分贝是贝尔的十分之一,但我们很少直接使用贝尔做单位。
[5] 音域是描述音高,即乐声或人声频率的特征,小提琴的音域在300至1400 Hz之间,大提琴的音域在70至750 Hz之间,低音提琴的音域在60至350 Hz之间。
[6] 波导是一种物理概念,指的是在一定距离内,将波限制在特定的区域中。波导现象通常广泛应用于光波和电磁波,一个典型例子就是光纤。而对于声波,特别是海水中的声波,波导的效果并不明显,因为尽管不同波长的声波在不同分层中的传播方式存在差异,但水下各层之间的分界却较为模糊。
[7] 图9中声源A和B之间的角度为90°,当声音频率为100 Hz时,d/λ=1/20,以人体中轴线计算,相移约为360/20=18°。18/90=1/5,这一比率体现了人类对空气中声音源头的敏感度。
环境百科全书由环境和能源百科全书协会出版 (www.a3e.fr),该协会与格勒诺布尔阿尔卑斯大学和格勒诺布尔INP有合同关系,并由法国科学院赞助。
引用这篇文章: MOREAU René (2024年4月12日), 声音的产生、传播和感知, 环境百科全书,咨询于 2025年4月26日 [在线ISSN 2555-0950]网址: https://www.encyclopedie-environnement.org/zh/physique-zh/emission-propagation-and-perception-of-sound/.
环境百科全书中的文章是根据知识共享BY-NC-SA许可条款提供的,该许可授权复制的条件是:引用来源,不作商业使用,共享相同的初始条件,并且在每次重复使用或分发时复制知识共享BY-NC-SA许可声明。









