| Focus 1/2 | The challenges of industrial hydraulic fracturing

Basic concepts of fracture mechanics

PDF

Until the beginning of the twentieth century, it was considered that the breaking strength of materials depended on extreme values of certain stress components. This was referred to as tensile strength or compressive strength.

In 1920, Griffith‘s [1] work on the development of fracture in metallic materials showed that in all materials, including glass, there are more or less small defects that involve local stress concentrations. Thus, the average stress values, calculated at any point of a material assuming that the material is homogeneous (without defects) and at rest (zero velocity at any point), do not make it possible to evaluate the loading conditions that cause the material to break. Attention should be paid to the growth of cracks and more particularly to the stress concentrations associated with them.

Today, the study of a rupture phenomenon must answer three questions:

  • What are the loading conditions that lead to the propagation of cracks?
  • What is the geometry of the surfaces generated by the propagation of these cracks?
  • Is the rupture process stable or unstable?

Propagation is stable when the growth of cracks stops spontaneously if the applied loads are kept constant. This is the case, for example, of cracks that can be seen in many masonry walls. Propagation is unstable if, when the applied loads are kept constant, there is an acceleration of the failure process. This instability gives rise to the propagation of mechanical waves. This is the case, for example, for fault failures that result in seismic movements. The question arises to identify the conditions that lead to the stabilization of a rupture that has become unstable. They are the ones who control, for example, the magnitude of earthquakes created during a fault failure.

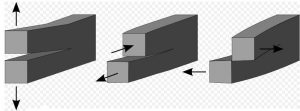
Encyclopedie environnement - mecanique rupture modes fondamentaux rupture
Figure 1. The 3 fundamental modes of rupture. Hydraulic fracturing is a pure tensile failure mode (mode I). Modes II and III are shear failure modes; they are often very unstable.

At the end of the 1950s, the metallurgist Irwin [2] proposed to consider the propagation of any crack as the superposition of three fundamental modes of failure (Figure 1):

  • Mode I corresponds to pure tensile propagation;
  • Mode II corresponds to a shear propagation in the plane of the figure;
  • Mode III corresponds to a shear propagation perpendicular to the plane of the figure.

These fundamental modes have been introduced because they allow an analytical calculation of the stress concentrations associated with them.

 

References and notes

[1] Griffith A.A., 1920. The phenomena of rupture and flow in solids; Phil. Trans. Roy. So. London; A 221, pp 163-198.

[2] Irwin, G.R., 1957. Analyses of stresses and strains near the end of a crack traversing a plate. J. App. Mech. , 24, 361-364.