Cooling comes from the sky

The cooling power of a surface exposed to the sky comes from the imbalance between the thermal radiation emitted and the radiation received from the sky – or, to be more precise, from the atmosphere. The radiation [26] corresponds to thermally excited molecules in the atmosphere. This thermal emission depends on the temperature and concentration of the molecules as well as their distance from the ground. It corresponds to an infrared emission centered on 10 µm.

1. Kirchoff’s law and black body

The thermal excitation of atoms and molecules of matter makes them vibrate, rotate and causes the emission of electromagnetic radiation. Let’s consider first a material of uniform temperature and composition called “black body” which absorbs and therefore emits all radiations according to Kirchoff’s law (Read: Thermal radiation of black body).

2. Stefan-Boltzmann law and emissivity of the material

The total radiative power P emitted by a surface element at the absolute temperature T can be obtained by integrating the spectral radiance of the black body on all wavelengths and on a half-space above the surface. We obtain the well-known formula P = σT4 where P is in W.m-2 and T in K; σ = 5.670×10-8 W.m-2. K-4 is the constant known as Stefan-Boltzmann.

For materials that do not absorb or emit all radiation, called “gray bodies”, the Stefan-Boltzmann law above must be corrected by what is called the emissivity of the material (The thermal radiation of black body). The emissivity has the same value as the absorptivity because both quantities correspond to symmetrical processes of emission and absorption of light between two states of molecular excitations [27]. For a gray body with emissivity ε < 1, the above Stefan-Boltzmann law becomes P = εσT4.

Note, however, that when dew begins to form, the substrate is wetted by water. It is then the emissivity of the water that matters. The emissivity of water is close to unity (0.98 in the atmospheric window, see below in section 3).

3. Emissivity of the atmosphere. Temperature of the sky

The atmosphere whose molecules absorb in specific spectral bands and emit radiation in the long-wave part of the spectrum (3-100 µm) is a gray body. Oxygen and nitrogen, which make up about 99% of the atmosphere, neither absorb nor emit far-infrared radiation; only water vapor (about 0.2% to 2% by volume) and carbon dioxide (about 0.03% by volume) contribute. The radiation of water vapor is therefore the most important. The strong absorption in this spectral region corresponds to a black body at a temperature of about 300K, except for a weaker absorption between 7 and 14 µm. The latter is known as the atmospheric window and contains no contribution from water. Only a peak due to stratospheric ozone is present, whose influence is relatively small due to the low temperature of the stratosphere. The concentration of water vapor generally decreases with altitude, making the atmospheric boundary layer [28] the place where most IR radiation is emitted to the ground. The boundary layer extends from a few tens of meters to a few kilometers.

We can also define an apparent sky temperature _Ts, which relates the ground air temperature _Ta and the sky emissivity εsto give the same sky radiance S as seen from the ground, by. We can easily deduce the sky temperature.

4. Cooling by radiative deficit

The radiative deficit R is the difference between the radiative power of the condensing surface material emitted to the sky and the power sent by the atmosphere when exposed to clear sky radiation. With material temperature Tc ≈_Ta, the air temperature, we have:

Since and materials cool below the air temperature. R is therefore the cooling power available for dew condensation. Since the emissivity of the sky depends primarily on the water vapor content of the atmosphere, the radiative deficit can be expressed as a function of the dew point temperature Tdor the relative humidity RH (defined in Focus Moist Air and Condensation). In Figure 1, Bliss (1961 [29]) describes the deficit as a function of T_a for several relative air humidities RH and T_d. For typical nighttime conditions where dew forms (T_a = 15°C and RH = 85% – 90%, T_d= 12.5 °C), R ≈ 60 W.m^-2.

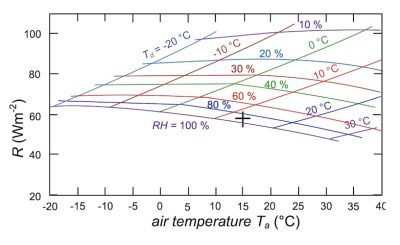
5. Angular dependence

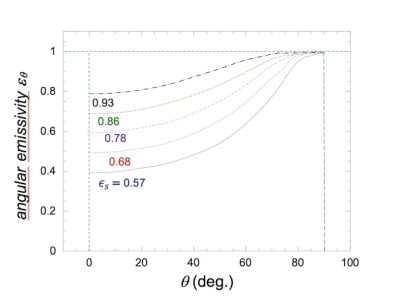
The emissivity estimated above is the total sky emissivity where all angles and wavelength contributions have been summed. However, there is a marked dependence of the sky emissivity with the zenith angle [30] θ (Figure 2), .

εs is the total emissivity. The emissivity is lowest for the atmosphere seen near the vertical(θ = 0 – 30°) corresponding to the smallest light path, and highest, near unity, near the horizontal(θ = 75 – 90°). For effective radiative cooling of a land surface, all angles less than about 15° above the horizontal should therefore be avoided. From the angle dependence of sky emissivity, the influence of the angle of inclination to the horizontal of the cooling material can be evaluated [31]. Not surprisingly, the radiative deficit is maximal for the horizontal position and minimal for the vertical position.

---

Notes and references

[Source: royalty free]

[26] RADIATION is the emission of energy by electromagnetic waves.

[27] MOLECULAR EXCITATION STATE: An excited state of an atom or molecule is a quantum state with a higher energy than the minimum, ground state (i.e. more energy than the absolute minimum). Excitations, for example by the absorption of light (a photon), increase the energy level above a chosen starting point, the ground state or an already excited state. The return to a less excited state corresponds to the emission of a photon (light) whose wavelength depends on the energy difference of the two states. For a thermal excitation at room temperature, the energy range corresponds to infrared wavelengths

[28] THE ATMOSPHERIC BOUNDARY LAYER includes the lowest part of the atmosphere that extends from the ground.) It is the place where the ground and the atmosphere exchange radiative, sensible and latent heat (See: Pressure, temperature and heat). It extends to where cumulus clouds form, which marks the beginning of the free atmosphere. In this layer, many physical quantities (air flow velocity, temperature, humidity…) show rapid and turbulent fluctuations and the vertical mixing is strong. The thickness of the boundary layer, h, can range from a few tens of meters to a few km and varies with time. It can be expressed by the following formula where H is expressed in km, T_a is the air temperature and Td the dew point temperature near the ground: H = (1/8)(T_a – T_d).

[29] BLISS R. A. (1961). Atmospheric radiation near the surface of the ground. Solar Energy 5 (3), 103-120

[30] BERGER, X., BATHIEBO, J. (2003). Directional spectral emissivities of clear skies. Renewable Energy 28 (12), 1925-1933.

[31] HOWELL, J.C., YIZHAQ, T., DRECHSLER, N., ZAMIR, Y., BEYSENS, D., SHAW, J.A. (2021). Generalized nighttime radiative deficits. Journal of Hydrology 603 (B), 126971.