Comment la matière se déforme : des fluides et des solides

Un cube de glace dans un verre est un solide élastique fragile, mais la Mer de Glace à Chamonix s’écoule comme un fluide visqueux. Effectivement, tout matériau peut passer d’un comportement solide à un  comportement fluide, et inversement, sous l’effet d’efforts mécaniques ou thermiques. Mais comment décrire ces deux états de la matière et les classes de comportement associées : élasticité, viscosité et plasticité ? Pourquoi de nouvelles variables, les contraintes et les déformations, sont-elles nécessaires pour décrire les efforts internes et les déformations de la matière?  Quelles sont les relations qui relient contraintes et déformations entre elles ? Pourquoi le calcul de structures ou d’ouvrages nécessite-t-il l’emploi de telles relations ? Voilà l’objet de cet article.

1. Des fluides et des solides

On distingue classiquement trois états de la matière : les gaz, les liquides et les solides. Mais d’autres états, plus complexes, existent aussi, comme les pâtes, les gels et les plasmas, dont nous ne parlerons pas dans cet article. Gaz et liquides sont proches du point de vue mécanique et on parle indistinctement de fluides. Cependant, dans une enceinte, les gaz, compressibles, occupent tout le volume disponible et leur comportement est bien décrit, en l’absence de réaction chimique, par leur loi d’état qui relie pression, volume et température (lire Pression, température et chaleur). Les liquides sont, quant à eux, quasi-incompressibles, bien qu’ils possèdent une certaine élasticité : ils subissent une petite variation de volume proportionnelle à la variation de pression. Dans une enceinte, les liquides vont occuper une partie du volume en adoptant la forme de cette enceinte.

Par ailleurs, on remarque qu’un fluide ne résiste pas à une pression appliquée si elle n’est pas isotrope (c’est-à-dire, identique dans toutes les directions de l’espace) : le fluide s’écoule. Ici, l’on rencontre une différence majeure avec les corps qualifiés de solides en ce sens qu’un échantillon solide parvient à résister à des forces de pression appliquées dans des directions différentes jusqu’à une certaine limite au-delà de laquelle le solide ne peut plus résister : il se casse. Un solide garde ainsi une forme propre, tandis qu’un fluide adopte la forme du récipient qui le contient (Figure 1).

De manière générale pour tous les matériaux, le comportement  le plus simple correspond à de petites déformations pour lesquelles la dissipation interne d’énergie en chaleur est négligeable. Dans ce cadre, lorsqu’on supprime les efforts appliqués, les déformations associées s’annulent aussi et le matériau reprend sa forme initiale. Ce comportement mécanique est dit réversible et tout comportement de ce type est qualifié d’élastique. Sinon, on parle d’inélasticité.

Nous venons de voir quelques caractéristiques générales des matériaux, qui peuvent se déformer sans perte d’énergie (les milieux élastiques) ou avec une dissipation d’énergie (les milieux inélastiques), s’écouler (les fluides) ou se casser (les solides). Ces différents comportements représentent ce qu’on appelle la « rhéologie » [1] du matériau. Si l’on veut pouvoir mener des calculs de structures (avions, voitures, machines, …) et d’ouvrages (routes, ponts, barrages, digues, …), ces notions vont devoir être d’abord précisées (section 2) puis formalisées (section 4). Mais cette formalisation va nécessiter au préalable d’avoir généralisé les concepts de forces et de déplacements. Ce sera l’objet de la section 3. Enfin, nous donnerons dans la section 5 un aperçu des calculs numériques modernes de structures et d’ouvrages et nous verrons pourquoi, pour l’ingénieur ou pour l’expert en géotechnique, le choix de lois de comportement, bien adaptées à tous les matériaux impliqués dans le calcul, est si crucial.

2. Élasticité, viscosité et plasticité

Notre expérience quotidienne montre que ces comportements élémentaires ne sont pas suffisants pour caractériser l’extrême variété de résistance des matériaux naturels ou industriels que l’on rencontre. Ainsi, une graisse industrielle va pouvoir résister à des pressions non-isotropes et ceci d’autant mieux que la vitesse, avec laquelle ces pressions sont appliquées, est grande. On dit que la graisse est visqueuse et, en première approximation, on peut supposer que la résistance de ce fluide est proportionnelle à la vitesse d’application de la pression. On parle alors de viscosité newtonienne. L’eau elle-même est aussi visqueuse, environ mille fois moins que l’huile, mais suffisamment pour expliquer une partie du frottement sur la carène des navires, où l’on note effectivement une résistance d’autant plus grande que la vitesse du navire augmente. Même les gaz, comme l’air, présentent une viscosité, 50 fois moindre que l’eau mais responsable, par exemple, de la persistance des nuages en freinant considérablement la chute des gouttelettes qui les constituent [2] (Lire Traînée subie par les corps en mouvement).

Les solides aussi peuvent présenter un comportement visqueux, par exemple lorsqu’ils se déforment dans le temps par un phénomène appelé fluage. Un fil de plomb auquel on suspend un poids va ainsi s’allonger progressivement au cours du temps, par fluage. Plus généralement, des échelles de temps différentes ou des variations de température peuvent transformer un fluide en solide ou inversement. Ainsi, un cube de glace se comportera comme un solide élastique-fragile à la sortie de son bac à glace. C’est en effet un solide puisqu’il a une forme propre, et, sous de faibles pressions appliquées, ses déformations reviennent à zero quand la pression s’annule – son comportement est ainsi réversible donc élastique. Par contre, sous un choc violent, il cassera brutalement, manifestant alors un comportement fragile. En revanche,  à l’échelle de l’année, la glace peut se comporter comme un fluide visqueux : ainsi, la langue de la Mer de Glace à Chamonix (Figure 2) s’écoule à raison d’environ 100 m/an en suivant les méandres de la vallée. On peut en déduire une estimation de sa viscosité : 10¹⁶ fois celle de l’eau.

Un cube de glace et un solide en général peuvent casser. Sa fracturation nette en plusieurs morceaux est appelée techniquement rupture fragile, comme on l’obtient avec un pic à glace pour la glace ou un marteau pour le verre.  Mais il existe une autre forme de rupture, pour laquelle le matériau ne se divise pas en fragments : c’est la rupture dite ductile, décrite par la théorie de la plasticité. Cette déformation plastique correspond principalement à des déplacements relatifs irréversibles des composants constitutifs du matériau, tels que blocs rocheux, grains de sable, particules argileuses, grains de poudres et de matériaux pulvérulents, cristaux d’un métal, cristaux de la glace …

Ces ruptures plastiques mettent en jeu des forces de frottement, internes aux matériaux, instantanées et indépendantes de la vitesse, selon la loi de frottement solide dite de Coulomb (Lire le focus Qu’est-ce que la loi de frottement de Coulomb ? associé à l’article sur le sable). Par contre, rappelons que, lorsque la déformation du solide est visqueuse, ces forces internes augmentent avec la vitesse de déformation. Ainsi le fil de plomb, évoqué plus haut, subira quasi-instantanément une élongation élastique (réversible) pour une faible charge, une élongation plastique (irréversible) pour une charge qui dépasse ce qu’on appelle le critère de rupture, et une élongation visqueuse (fluage) proportionnelle au temps pour une charge plus faible qui persiste. Le fer peut subir également des déformations plastiques, et ce d’autant plus facilement que sa température est élevée : il devient ainsi ductile. Le forgeron connait bien ce phénomène qui lui permet de déformer profondément une pièce métallique sans la casser en fragments. Le métal flue ainsi d’autant mieux que la température augmente, et, à la température de fusion, il change d’état et se transforme en un liquide ordinaire, guère plus visqueux que l’eau.

En somme, les déformations plastiques sont instantanées, tandis que les déformations visqueuses sont différées (étalées dans le temps). L’empreinte d’un pied sur le sable de la plage est à la fois instantanée et irréversible (permanente) : on peut donc qualifier ici le comportement du sable de « plastique ». Celle d’un pied dans un champ boueux sera irréversible mais augmentera au cours du temps (si l’on se fige sur place suffisamment longtemps !) par fluage : le comportement de l’argile sera ici visqueux. Quant aux déformations parfaitement réversibles, qui s’annulent quand la charge s’annule, nous avons vu qu’elles sont décrites par la théorie de l’élasticité. En somme, les déformations réversibles relèvent de l’élasticité ; les déformations irréversibles relèvent de la viscosité lorsqu’elles sont fonction du temps ; elles relèvent de la plasticité si elles sont indépendantes du temps.

Aujourd’hui, il est souvent admis qu’il n’existe pas de matériaux intrinsèquement solides, mais plutôt des domaines de comportement à caractéristiques solides ou fluides pour un matériau donné, dont le comportement général sera de type élasto-visco-plastique. A titre d’illustration, prenons encore le cas du sable : solide élasto-plastique, sur lequel on marche sur la plage, et fluide granulaire, qui s’écoule dans un sablier (Figure 3).

3. Contraintes et déformations

Le mouvement d’un objet matériel assimilable à un point est entièrement décrit par les notions de vecteur force et de vecteur déplacement, reliés par les lois de la dynamique (Lire Les lois de la dynamique). Selon ces lois, la force appliquée est égale au produit de la masse de cet objet par son accélération. Par ailleurs, un fluide, gaz ou liquide, est caractérisé en première approximation par sa pression et son volume (si l’on ne prend pas en compte les aspects thermiques), reliés par une loi d’état.

Considérons maintenant un solide déformable et voyons pourquoi les notions précédentes de force-déplacement ou de pression-volume ne s’appliquent plus et doivent être généralisées. Prenons l’exemple d’un seau rempli de sable. Si nous lui appliquons une pression verticale en appuyant sur la surface libre supérieure, l’expérience montre qu’on mesure environ la moitié de cette pression sur les faces latérales du seau et un peu moins que cette pression sur le fond du seau. Si le seau avait été rempli d’eau, on aurait recueilli la même pression partout : l’eau a un comportement isotrope, mais ce n’est pas le cas du sable. Il a donc fallu imaginer un nouvel outil mathématique pour décrire cette pression dans un solide déformable, qui varie avec la direction au sein du solide, ou plus exactement avec l’orientation de toute facette, que l’on peut isoler par la pensée au sein du solide et sur laquelle s’exerce cette pression. La notion de vecteur ne permet pas de décrire cette variation directionnelle de la force par unité de surface. L’outil qui permet cette description est un tenseur [3] d’ordre 2. Nous allons voir comment le construire.

Sur chacune des faces du cube de la figure 4 s’exerce un ensemble de forces, pas nécessairement perpendiculaires à la face. Il faut ainsi généraliser la notion de pression (toujours perpendiculaire à la surface dans le cas d’un fluide statique) en considérant des efforts obliques par rapport à la surface. Le seul fait que l’on puisse marcher sur le sol sans glisser montre que l’on peut effectivement appliquer des efforts tangentiels sur la surface d’un solide et que celui-ci peut y résister. D’après le principe de l’action et de la réaction, les six forces représentées sur les faces du cube de la figure 4 sont égales deux à deux sur des faces opposées. Il n’existe donc que trois vecteurs forces indépendants. Ces trois forces par unité de surface, appelées vecteurs contraintes, permettent de construire une matrice carrée de 3 lignes et 3 colonnes : c’est la matrice des composantes du tenseur de contrainte. On montre qu’elle permet de calculer la force surfacique qui s’exerce sur toute facette, d’orientation quelconque, à l’intérieur du matériau.

Ainsi dans ce cas du seau de sable, la contrainte verticale dans le seau sera égale à :

σ_v =  F / S , où F est la force verticale totale appliquée et S la surface d’une section horizontale du seau. La contrainte horizontale ou radiale, appliquée sur les parois latérales du seau, sera, elle, approximativement égale à :

σ_h = σ_v / 2 =  F / 2S.

Ces deux contraintes sont dites principales, car elles s’appliquent perpendiculairement aux facettes respectives horizontales et latérales.

Dans le cas d’une orientation quelconque de la facette, les vecteurs contraintes ne lui sont pas perpendiculaires. On distingue alors le vecteur contrainte projeté sur le plan de la facette – appelé contrainte de cisaillement  ou contrainte tangentielle – et celui projeté perpendiculairement à ce plan, sur la normale à la facette – appelé contrainte normale (voir la figure 5).

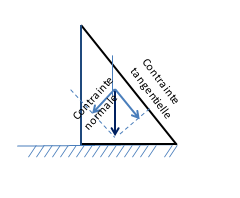
Revenons maintenant à la notion de déplacement d’un point matériel ou de variation de volume d’un matériau, qu’il nous faut aussi généraliser. Effectivement, l’expérience menée sur le seau rempli de sable montre que la surface supérieure libre du sable se tasse sous l’action de la pression verticale exercée par la main, tandis que les surfaces latérales, maintenues par le seau, restent fixes. Là aussi, il apparait que les déplacements de ces surfaces ne sont plus identiques dans toutes les directions de l’espace comme dans le cas d’un fluide, mais au contraire qu’ils varient avec ces directions.

Si l’on assimile chaque petit volume de sable à un point matériel, on obtient ce qu’on appelle un champ de déplacements, décrivant le déplacement de tout point matériel du sable – concrètement, de tout grain de sable – dans le seau. Une question se pose ici. Dans la direction verticale du seau, les déplacements vont être importants près de la surface libre et nuls au fond du seau. Ils vont en fait varier linéairement avec la profondeur. Pourtant, chaque petit cube, soumis à la même pression verticale, se « déforme » verticalement de la même manière. Il nous faut donc passer de la notion de « déplacement » à la notion, plus intrinsèque, de « déformation ». Cela se fait par une opération de gradient[4], qui transforme le déplacement vertical en une quantité adimensionnelle appelée « déformation verticale », identique en tout point du sable et égale au rapport du déplacement vertical d’un grain de sable par la hauteur de ce grain dans le seau.

Mais il nous faut généraliser cette expérience, car que se passerait-il si les parois du seau se déformaient sous l’action de la pression verticale exercée sur la surface libre du sable ? Alors, les déplacements des grains de sable ne seraient plus verticaux mais obliques. En prenant alors le gradient de ce champ de déplacements (vecteurs à 3 composantes), on obtient un champ de matrices déformations (à 3 lignes et 3 colonnes) caractérisant complètement la déformation du sable dans un seau déformable.

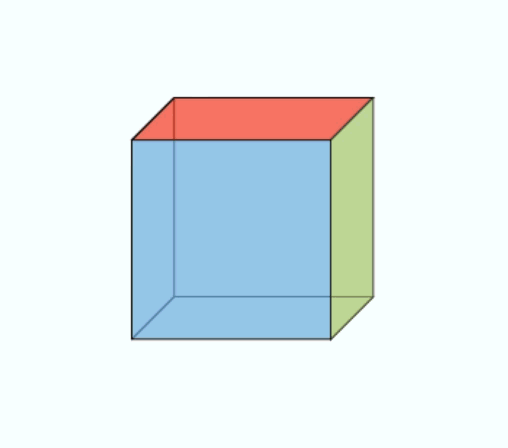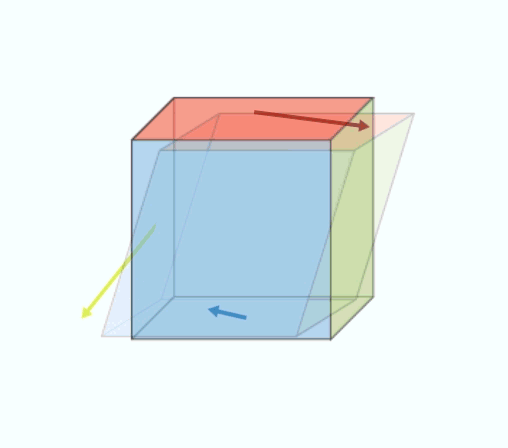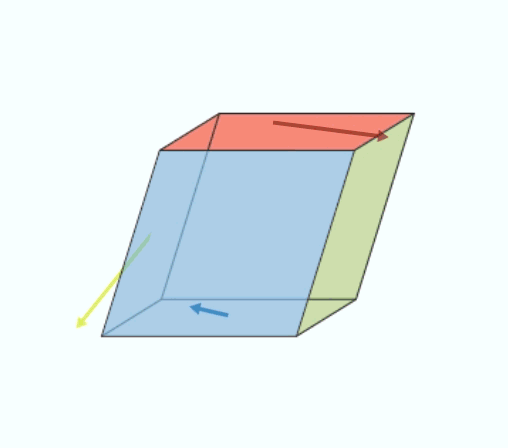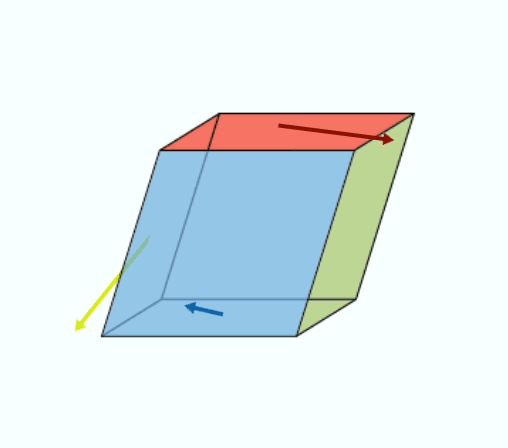
Cette matrice carrée de 3 lignes et 3 colonnes peut en fait être décomposée en la somme de deux matrices : l’une décrit la rotation du cube de matière durant l’application des efforts et l’autre la déformation proprement dite du cube (sans rotation), c’est ce que l’on appelle la déformation pure (voir une illustration sur la figure 4).

Sur l’exemple simple du seau de sable à parois rigides, la déformation verticale est égale à : ε_v =  δH / H , où H est la hauteur du seau, tandis que la déformation horizontale ou radiale vaut : ε_h = δD / D, où D est le diamètre du seau. Ces déformations sont dites principales, car elles sont perpendiculaires aux surfaces respectives horizontale et verticale ou latérale.

En fait, de manière générale, on montre que la déformation pure permet de retrouver les deux modes fondamentaux de déformation d’un cube élémentaire de matière soumis à des efforts quelconques: la longueur d’un segment matériel à l’intérieur du cube change et l’angle entre deux segments matériels varie également au cours de la déformation du cube.

Ce sont les Égyptiens qui, les premiers, ont défini ces deux notions de longueur et d’angle, qui leur permettaient de retrouver les limites de leurs champs, recouverts par les limons des crues du Nil, après le passage de ces crues. Aujourd’hui encore, nous continuons à nous représenter la déformation de la matière à travers ces deux notions, et, précisément, on montre que la déformation pure nous fournit ces deux quantités en tout point d’un matériau déformable.

4. Lois de comportement

Chaque matériau se déforme d’une manière qui lui est propre et qui caractérise ce que l’on appelle son comportement mécanique, formalisé par une relation mathématique appelée « loi de comportement ». De manière générale, la contrainte en un point donné du matériau et à un instant donné est fonction de toute l’histoire de la déformation pure en ce point.  Dans le cas d’un comportement élastique, une simple fonction mathématique (indépendante de toute histoire) relie la contrainte à la déformation.

L’élasticité est dite linéaire, si cette fonction est linéaire et une relation de proportionnalité relie alors contraintes et déformations : la matrice contrainte est, dans ce cas, égale au tenseur élastique multiplié par la matrice déformation. Dans le cas usuel de matériau élastique isotrope (son comportement est identique dans toutes les directions de l’espace), ce tenseur dépend de deux paramètres seulement : le Module de Young (caractérisant la raideur du matériau) et le Coefficient de Poisson (traduisant son aptitude à se déformer latéralement sous compression axiale).

La viscosité newtonienne, la plus simple des lois visqueuses, se traduit quant à elle par une relation de proportionnalité entre la contrainte et la vitesse de déformation pure au même instant. Ce type de relation permet ainsi de décrire l’augmentation de la résistance du matériau avec la vitesse d’application des efforts.

Enfin, en élasto-plasticité, cette relation entre contrainte et déformation n’est plus univoque comme en élasticité pure et on préfère alors utiliser une écriture dite  incrémentale reliant une petite variation de contrainte à une petite variation de déformation. On fait ainsi apparaître un tenseur élasto-plastique, reliant la contrainte incrémentale à la déformation incrémentale de manière proportionnelle. Le matériau qui obéit le plus fidèlement à un comportement élasto-plastique est le sable. Ainsi, un tas de sable ou une dune à l’équilibre présente une pente (Figure 6), dont l’angle (autour de 30°) correspond au frottement plastique interne entre les grains de sable. Un liquide visqueux, dénué de plasticité, s’étalerait au contraire progressivement, de manière différée dans le temps. Le comportement plastique du sable permet à la pente d’être stable sans étalement. Cependant, si on ajoute un peu de sable le long de la pente, une avalanche locale se produit immédiatement, manifestant le fait que l’état mécanique du sable correspond ici à un état de plasticité dit « limite » correspondant au critère de rupture évoqué dans la section 2 : cet angle limite de pente ne peut pas être dépassé.

Une des propriétés intéressantes de la plasticité est le phénomène d’écrouissage, qui traduit la possibilité d’améliorer la résistance mécanique d’un matériau en le déformant plastiquement. Une illustration remarquable en est la mise en œuvre de la sous-couche d’une chaussée. Le sable est déversé par camions et son état, très lâche, ne lui permet alors qu’une très faible résistance : un doigt peut s’y enfoncer. Mais, une fois compactée par des rouleaux compresseurs qui l’écrouissent très fortement, la couche de sable devient remarquablement résistante : une voiture peut déjà rouler sur cette couche. Par contre, en l’absence de colle entre les grains de sable, elle aura du mal à freiner car les grains de sable n’offriront pas une résistance suffisante au glissement des pneus. C’est le bitume qui fournit cette colle : il assure la cohésion du sable ou de son mélange avec des graviers. Mais, par ailleurs, cette cohésion crée la possibilité de fissurations, qui dégradent la chaussée …

On comprend ici les difficultés numériques intrinsèques au calcul d’une structure métallique, au dimensionnement d’un ouvrage de génie civil, à la prévision de l’écoulement d’un fluide complexe ou plus généralement du comportement de tout système mécanique, tant il est vrai que le comportement élasto-visco-plastique des matériaux est complexe à calibrer expérimentalement et à décrire numériquement. Mais comment peut-on précisément calculer – c’est-à-dire in fine prédire – le comportement mécanique d’un système soumis à des efforts qui peuvent être variables au cours du temps ?

5. Résolution d’un problème de mécanique des matériaux déformables

Que l’on considère des fluides ou des solides, pour calculer et prévoir le comportement d’une structure et d’un ouvrage, l’ingénieur est amené à écrire et à résoudre trois groupes d’équations mathématiques de nature très différente :

• Les lois de conservation (de la masse, de l’énergie, de la quantité de mouvement, etc.), valables quels que soient le matériau et le problème considéré. Ces lois sont généralement connues et formalisées depuis fort longtemps.
• Les lois de comportement des matériaux dont nous avons décrit la formalisation dans cet article. Ces lois qui relèvent, dans le cas le plus général, de l’élasto-visco-plasticité comme nous l’avons vu, font toujours l’objet de recherches actives et incorporent aujourd’hui une description fine de la microstructure des matériaux (et même de leur nano-structure, quand on considère aujourd’hui des nano-matériaux).
• Les conditions initiales et les conditions aux limites qui définissent le système, la structure mécanique, l’ouvrage, l’écoulement, etc., que l’on cherche à modéliser. Les conditions initiales caractérisent l’état initial (au début du calcul) du système. Les conditions aux limites, quant à elles, fixent toutes les géométries et les efforts qui seront appliqués au cours du temps. Les codes de calculs industriels sont actuellement en mesure de prendre en compte une très grande variété de telles conditions.

Parfois plusieurs phases physicochimiques sont présentes (par exemple, le sol, l’air et l’eau, ou bien la roche, le pétrole et le gaz) et on parle alors de milieux multi-phasiques. Dans d’autres cas, le problème fait apparaître des chargements « couplés ». Il s’agit alors de problèmes dits multi-physiques (par exemple, couplage entre mécanique et thermique si la température intervient, ou couplage entre mécanique et chimie dans le cas de réactions chimiques entre les constituants du système, etc.).

Pour l’ingénieur, la question la plus délicate réside le plus souvent dans le choix et la mise en œuvre de lois de comportement, aussi représentatives que possible des matériaux concernés dans le problème considéré. Les méthodes numériques modernes permettent de résoudre le système d’équations formé par les trois groupes d’équations évoquées plus haut. Le nombre d’équations peut atteindre plusieurs millions et impose alors d’utiliser des super-calculateurs.

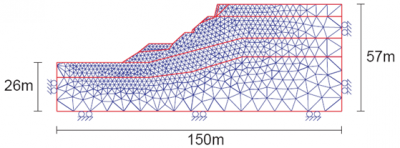
Si l’on peut supposer que la continuité de la matière est respectée au cours de sa déformation, la méthode la plus connue est celle dite des « éléments finis » (Figures 7 et 8). Le calcul présenté sur ces deux figures a permis de modéliser numériquement, et donc de comprendre, un glissement de terrains qui s’est effectivement produit à Trévoux après des pluies torrentielles (lire Les glissements de terrains).

Aujourd’hui on pourrait quantifier la pluviométrie critique. Des dispositifs de prévention (murs, remblais, renforcement des sols, drainage, …) peuvent aussi être numériquement testés pour valider ou pas leur efficacité. Par contre, si les matériaux présentent des discontinuités intrinsèques et irréductibles (par exemple, en cas de fracturation de la matière comme dans le cas d’une falaise fracturée), on peut faire appel à une autre méthode numérique dite aux « éléments discrets » (Figure 9). On obtient alors par calcul numérique les déplacements et rotations de chaque bloc élémentaire, qui peuvent être au nombre de plusieurs millions. Par exemple, la fragmentation d’un bloc de béton impacté par un projectile peut être simulée numériquement. Cette méthode permet aussi le calcul des avalanches (de neige, de blocs rocheux, …) et celui des coulées de boues torrentielles.
(Lire Glissements et éboulements rocheux, une fatalité ?).

 

---

Références et notes

Image de couverture. Le pont haubanné de Millau est un exemple d’ouvrage dont la conception a nécessité des études approfondies sur le comportement des matériaux qui le constituent. [Source : Wikipédia, Licence Paternité – Partage des conditions initiales à l’identique v. 2.5 de Creative Commons, plus connue sous le nom de « CC‑BY‑SA‑2.5 ; © Mike Lehmann, Mike Switzerland 10:38, 14 March 2008 (UTC) ».

[1] La rhéologie est la science qui décrit comment la matière s’écoule ou, plus généralement, se déforme. Le mot est issu du grec « ρεω » qui signifie « s’écouler » et de  « λοϒοσ » « discours ».

[2] Dans le cas de véhicules ou autres objets de grande dimension la résistance à l’avancement est dominée par la turbulence et la viscosité intervient peu.

[3] Un tenseur est un objet mathématique qui respecte les règles dites de tensorialité. Ces règles permettent de continuer à décrire le même être physique, quel que soit le repère d’expression que l’on a choisi pour exprimer ses composantes. Les composantes d’un tenseur d’ordre 1, qui est un vecteur, forment une ligne ou une colonne de chiffres ; celles d’un tenseur d’ordre 2 forment une matrice (tableau de chiffres). Contraintes et déformations sont ainsi représentées à l’aide de matrices. On définit des tenseurs d’ordre fini quelconque. Par exemple, le tenseur élastique (dont on parlera plus loin) est d’ordre 4.

[4] Le gradient d’une fonction scalaire est un vecteur dont les composantes sont les dérivées partielles de la fonction par rapport aux coordonnées spatiales. Par extension, le gradient d’un vecteur est une matrice dont les vecteurs-colonnes sont constitués des dérivées partielles de chacune des composantes du vecteur par rapport aux coordonnées spatiales. Dans l’espace classique à 3 dimensions, on obtient ainsi une matrice carrée de 3 lignes et 3 colonnes.