La diffusion, étape ultime d’un bon mélange
PDF
Les espèces chimiques comme le dioxyde de carbone (CO2) dans l’air, ou le sucre dans le café, finissent, au bout d’un certain temps, par être intimement mélangées au fluide environnant, même s’il est au repos. Le même mécanisme assure le transport de la chaleur à travers les corps immobiles, jusqu’à ce que leur température soit uniforme. De façon analogue, dans une couche fluide soumise à un frottement, l’effort exercé en surface est transmis dans toute son épaisseur. Dans les milieux fluides, la turbulence disperse les constituants, mais sans atteindre les échelles moléculaires ; c’est l’agitation désordonnée des molécules qui achève ce processus de transport appelé la diffusion. Nous verrons qu’à lui seul il serait extrêmement lent mais que la turbulence l’aide de façon efficace.
Le mot diffusion est utilisé avec des significations relativement variées. Ce qui est commun à toutes les situations, c’est le fait qu’une certaine grandeur soit transportée à travers un milieu dispersé par l’agitation des particules élémentaires qui le constituent. En physique, on distingue deux familles de phénomènes de diffusion :
- Un phénomène de transport qui s’appuie sur les propriétés du milieu considéré, constitué d’atomes ou de molécules en agitation désordonnée. Il est caractérisé par le fait que la distribution de la grandeur transportée tend à devenir uniforme ; cette grandeur peut être la concentration d’une espèce chimique particulière, la chaleur ou la quantité de mouvement. L’état ultime uniformisé constitue l’équilibre thermodynamique du milieu.
- Le phénomène de diffraction des ondes dans un milieu non homogène, que ces ondes soient électromagnétiques comme la lumière ou acoustiques comme le son. Ces phénomènes sont décrits dans d’autres articles de cette encyclopédie : Les couleurs du ciel, Emission, propagation et perception du son. Dans la langue anglaise ce phénomène de diffraction des ondes est désigné par le mot scattering, qui le distingue de la diffusion proprement dite.
Dans le langage courant le même mot, diffusion, est utilisé avec des significations encore différentes. Ainsi, il peut désigner le transfert de connaissances vers un grand nombre de personnes ; il peut aussi désigner la transmission d’informations variées par radio (on parle de radiodiffusion) ou télévision (on parle alors de télédiffusion).
- 1. L’air au repos : un ensemble agité de molécules
- 2. Des paramètres moléculaires aux propriétés macroscopiques d’un gaz, ou l’inverse
- 3. Le mécanisme de la diffusion dans les gaz
- 4. La diffusion turbulente
- 5. Diffusivité massique et diffusivité thermique
- 6. Diffusion du mouvement : la viscosité
- 7. Le mécanisme de la diffusion dans les liquides
- 8. Messages à retenir
1. L’air au repos : un ensemble agité de molécules
Dans l’article L’atmosphère et l’enveloppe gazeuse de la Terre, les principaux constituants de l’air sec sont cités : azote (71%), oxygène (28%), argon (moins de 1%), ainsi que quelques autres gaz en proportions beaucoup plus faibles. Cet ensemble est constitué de molécules, qui occupent tout l’espace disponible, propriété spécifique des gaz, qui les distingue des états condensés de la matière (liquide ou solide). Ceux-ci ont en effet un volume propre, les solides ayant aussi une forme propre.


2. Des paramètres moléculaires aux propriétés macroscopiques d’un gaz, ou l’inverse
Il est assez simple de relier ces paramètres du monde moléculaire à quelques grandeurs macroscopiques, mesurables et accessibles à nos sens. Ces grandeurs – analysées dans l’article Pression, Température et chaleur – sont la pression p, la température T, la masse de l’unité de volume (ou masse volumique) ρ et la viscosité [3] μ. Pour cela, nous disposons d’une première relation presque évidente entre les échelles moléculaires et les échelles macroscopiques : la masse m est le quotient m = M/NA entre la masse molaire M et le nombre d’Avogadro (nombre de molécules par mole) NA = 6,022×1023 mol-1. Par ailleurs, la masse volumique ρ doit être égale au produit du nombre n de molécules présentes dans l’unité de volume multiplié par la masse de chacune. Nous disposons donc d’une deuxième relation entre les paramètres des deux mondes : ρ = nm.
Pour relier la pression p en un point du milieu gazeux à ses paramètres moléculaires, imaginons qu’une surface solide plane d’aire unité (S = 1, quel que soit le système d’unités choisi) soit placée quelque part dans ce milieu gazeux. Chacune des deux faces de la surface va recevoir et cumuler les impulsions de toutes les molécules qui vont la frapper pendant l’unité de temps, venant de toutes les directions, perdant et regagnant leur énergie cinétique, de l’ordre de mc2/2 pour chacune d’elles. En moyenne, la force exercée sur la surface unité et égale à p doit donc être de l’ordre de nmc2. Un calcul rigoureux, tenant compte des vitesses réelles des molécules rencontrées [4], conduirait à l’expression p = nmc2/3. On obtient au passage une évaluation de l’erreur due aux hypothèses simplificatrices du modèle adopté : le coefficient 1/3. L’important ici est le fait que nous ayons obtenu une troisième relation entre les paramètres moléculaires (n, m, c) et une propriété macroscopique, la pression p.
Dès lors que la pression et la masse volumique sont reliées aux paramètres moléculaires, il suffit -pour exprimer la température- d’identifier la pression p exprimée ci-dessus avec celle qui vérifie l’équation d’état des gaz parfaits : p/ρ = RT/M, où R = 8,314 m3.Pa.mol-1.K-1 désigne la constante universelle des gaz parfaits et M la masse molaire moyenne du mélange gazeux. On obtient la quatrième relation [5] T = Mc2/3R qui met en évidence la proportionnalité entre la température T et le carré de la vitesse des molécules c2 (Lire Pression, température et chaleur).
À ces quatre relations ajoutons celle qui exprime la viscosité dynamique du gaz, qui est établie plus loin dans la section 5 : μ = nmcλ/3. Alors, avec les valeurs suivantes, usuelles pour l’air au niveau de la mer
p = 1,013 105 Pa, T = 288 K, ρ = 1,22 kg.m-3, ν = 10-5 m2.s-1,
les cinq relations citées conduisent à :
n = 2,5 ×1025 m-3, m = 4,8 × 10-26 kg, c = 497 m.s-1,
d = 3,4 × 10-9 m, σ = 0,46 × 10-9 m, λ = 6 × 10–8 m.
Pour se faire une idée assez juste des échelles du monde moléculaire, on pourra remarquer que le nombre de molécules contenues dans un petit cube d’un micron de côté est de l’ordre de 25 millions. On en déduira que la distance typique entre deux molécules voisines (d) est de l’ordre de 7 fois leur diamètre (σ), que leur libre parcours moyen (λ) est de l’ordre de 60 nanomètres, soit environ 130 fois leur diamètre, et que la vitesse moyenne des molécules est légèrement supérieure à la célérité du son (340 m.s-1).
3. Le mécanisme de la diffusion dans les gaz

Toutefois, le temps nécessaire pour établir cet équilibre est beaucoup plus long (des heures ou davantage) que la durée entre deux collisions moléculaires (de l’ordre de λ/c ≈ 1,4×10-10 s). Dans ces conditions, les collisions sont tellement fréquentes autour d’un point donné, que l’on peut admettre que les molécules qui partent du voisinage de ce point après une collision portent toutes la même valeur de G, à savoir G/n puisque G désigne la valeur par unité de volume. On dit alors que ce gaz est dans un état d’équilibre local.
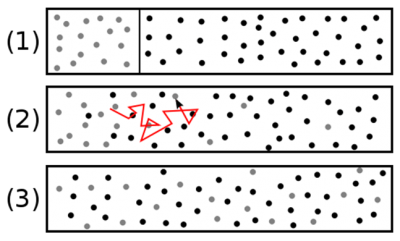
Les molécules qui traversent une unité de surface plane perpendiculaire à la direction x (retour à la Figure 3) portent, en moyenne, la grandeur G/n. La distance d’où elles viennent est de l’ordre d’un libre parcours moyen λ. La petitesse de cette longueur λ par rapport aux dimensions macroscopiques justifie que l’on suppose linéaire, avec une pente Γ0, la distribution G(x) au voisinage de la coupe située à x = 0. Ceci conduit à la distribution simple : G = G0 + Γ0 x. Admettons même que les molécules qui viennent du côté x>0 portent toutes G+ = G0 + Γ0λ, et que celles qui viennent du côté x<0 portent G– = G0 – Γ0λ.
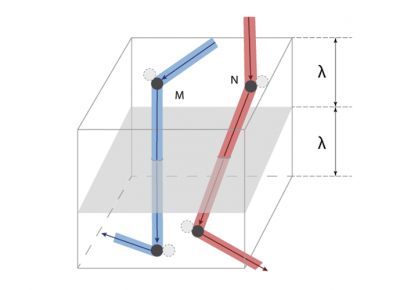
Finalement, le débit φ de G à travers chaque unité de surface du plan x = 0 peut être estimé par la relation φ = (cλ/3) dG/dx. La conclusion de cette estimation est la suivante : si une grandeur G est distribuée de façon non uniforme, le débit net de G transporté par l’agitation moléculaire est proportionnel au gradient local dG/dx et s’exprime par une relation de la forme φ = -D dG/dx, où, par convention, on place le signe – pour que le flux soit positif lorsque dG/dx est négatif (la chaleur va du côté chaud vers le côté froid). Le coefficient D apparaissant dans cette relation vaut D = cλ/3. Il est appelé la diffusivité de ce gaz ; c’est une grandeur purement cinématique qui se mesure en m2/s. Il est remarquable que l’on ait pu évaluer la diffusivité du gaz sans spécifier la nature de la grandeur transportée.
Les valeurs numériques indiquées en section 2 permettent d’estimer la diffusivité de l’air. Avec c = 497 m s-1 et λ = 6 × 10–8 m, on obtient : D ≈ 10-5 m2 s-1. Pour donner à cette valeur une signification pratique, revenons à l’expérience de la figure 4. Si l’on note L la longueur de l’enceinte, puisque la diffusivité possède la dimension d’une longueur au carré divisée par un temps (L2T-1), la durée typique pour atteindre l’état final en équilibre est nécessairement de l’ordre de L2/D. Si L ≈ 10 cm, cette durée est de l’ordre d’une heure. Pour que cette durée soit de l’ordre de la seconde, il faudrait que l’enceinte de la figure 4 ait une longueur voisine du millimètre, ce serait le cas d’une petite bulle.
4. La diffusion turbulente
Dans la plupart des milieux fluides de notre environnement, notamment l’air et l’eau, la turbulence est presque omniprésente. C’est un phénomène d’agitation totalement étranger au mouvement des molécules. Au sein d’un écoulement comme le vent, ou comme un courant marin, il se manifeste par la présence de fluctuations de vitesses à grande échelle, assez importantes et aisément mesurables. Même sans écoulement imposé, en présence d’une instabilité hydrodynamique [6], la turbulence est présente sous la forme d’un ensemble de tourbillons de toutes tailles intriqués les uns dans les autres. On peut voir une certaine analogie avec l’agitation moléculaire décrite dans les sections précédentes, mais aux échelles des tourbillons, beaucoup plus grandes que le libre parcours moyen des molécules. Cette analogie a amené Prandtl [7] à supposer que l’on pouvait définir une longueur de mélange [8], analogue au libre parcours moyen des molécules d’un gaz.
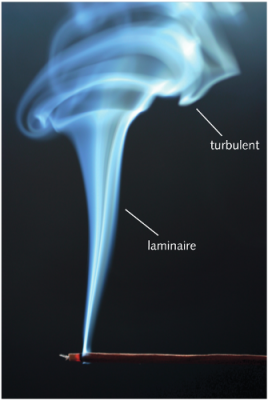
[Source : © Krunoslav Knezevic]
Le concept de longueur de mélange, grandeur notée l ci-dessous, est assez flou mais il a le mérite de permettre de dégager des ordres de grandeurs satisfaisants. La situation où il est le mieux justifié est celle d’une couche limite (voir figure 7). L’expression suggérée par Prandtl dans une telle couche limite et généralement adoptée est l = κy, où y est la distance à la paroi et κ une constante numérique déterminée par l’expérience. Avec cette expression de la longueur l, l’ordre de grandeur des fluctuations de vitesse à la distance y de la paroi peut être estimé par u’ ≈ l dU/dy. L’analogie avec l’agitation des gaz suggère de réutiliser l’expression de la diffusivité moléculaire (D = cλ/3) en remplaçant c par u’ et λ par l = κy. La diffusivité turbulente Dt au sein d’une couche limite devient alors : Dt ≈ u’l ≈ κ2y2 dU/dy.
A titre d’exemple, plaçons-nous au sein de la couche limite atmosphérique, dont l’épaisseur est de l’ordre de quelques centaines de mètres, à une distance du sol y ≈ 10 m où la vitesse moyenne est voisine de 10 m.s-1 et où dU/dy ≈ 1 s-1. En adoptant pour la constante κ la valeur 0,1, tirée des expériences, ces estimations conduisent à une diffusivité turbulente Dt ≈ 10 m2.s-1, soit un million de fois supérieure à la diffusivité moléculaire. Cette valeur réduit à environ un dixième de seconde la durée nécessaire pour réaliser le mélange turbulent : t ≈ l2/Dt ≈ 0,1 s. Mais ce mélange n’est pas achevé car les constituants ne sont dispersés que jusqu’à l’échelle des plus petits tourbillons, laquelle dépend de la viscosité du fluide. Dans le cas de la couche limite atmosphérique celle-ci est voisine du millimètre. C’est l’agitation moléculaire qui achève le mélange jusqu’aux dimensions moléculaires, et nous savons que cela requiert une durée L2/D. En réalité la diffusion moléculaire commence au sein des tourbillons millimétriques où elle coexiste avec la dispersion turbulente. Pour simplifier, admettons que la diffusion moléculaire agit seule au-dessous du millimètre. Avec L ≈ 10-3 m et D ≈ 10-5 m2 .s-1, on obtient encore une durée de l’ordre du dixième de seconde.
On pourra retenir de ces estimations que :
- la diffusion turbulente ne fait que disperser les constituants jusqu’à l’échelle des petits tourbillons,
- la diffusion moléculaire achève ce mélange,
- les durées des deux mécanismes peuvent avoir des ordres de grandeurs voisins, de l’ordre du dixième de seconde,
- sans turbulence, la durée nécessaire pour réaliser un bon mélange pourrait atteindre plusieurs heures.
5. Diffusivité massique et diffusivité thermique
C’est par l’expression diffusivité massique que l’on désigne habituellement la diffusivité d’une espèce chimique contenue dans le milieu fluide. Supposons donc que, parmi les molécules du fluide considéré, gaz ou liquide, certaines soient différentes des autres. Prenons l’exemple des molécules d’eau (H20) sous forme de vapeur, dans un air absolument calme au-dessus d’une grande étendue liquide, comme celle d’un lac paisible. Et notons maintenant C la concentration volumique de l’eau dans l’air à toute altitude z, grandeur initialement notée G avant que sa nature soit précisée. Pour évaluer le flux net de vapeur d’eau vers les hautes altitudes, la loi vue précédemment conduit à l’expression φ = -D dC/dz. C’est la loi de Fick. Elle est indispensable pour pouvoir calculer la quantité d’eau extraite par diffusion des basses altitudes, mais il faut la compléter par un bilan massique et par des conditions initiales et aux limites.
On réserve l’expression diffusivité thermique pour le transport de chaleur par l’agitation moléculaire. Supposons maintenant que la grandeur G soit l’énergie interne E par unité de volume du gaz, dont toute variation infinitésimale dE se manifeste par une variation de température dT, suivant la loi dE = ρCv dT, où Cv désigne la capacité calorifique à volume constant du gaz. Alors le transport par diffusion de cette énergie interne, c’est-à-dire de la chaleur, devient φ = -ρCvD dT/dz. Il est habituel d’écrire cette expression appelée loi de Fourier sous l’une des deux formes suivantes : φ = -k dT/dz, où k = ρCvD = Cv nmcλ/3 est appelé la conductivité thermique du gaz, ou encore φ = -α ρCp dT/dz, où α = k/ρCp désigne bien la diffusivité thermique du gaz. La grandeur Cp désigne alors la capacité calorifique à pression constante du gaz.
Les propriétés physiques des gaz, notamment de l’air, introduites plus haut (D, k, α, μ, ν) sont liées aux paramètres moléculaires n, m, c et λ. Parmi eux, pour un gaz de masse volumique donnée, seule la vitesse des molécules c est susceptible de varier avec la température T. Et l’on a vu que cette dépendance pouvait s’écrire : T = Mc2/3R = mc2/3kB. On peut en déduire que les diffusivités d’un gaz (D, k, α, μ, ν) varient comme la racine carrée de sa température.
6. Diffusion du mouvement : la viscosité
Admettons maintenant que les notions précédentes demeurent valables dans un fluide mis en mouvement aux échelles macroscopiques par le déplacement d’une paroi dans son propre plan. Cette hypothèse est très bien justifiée tant que les durées typiques du mouvement macroscopique (des secondes ou des minutes, en général) sont considérablement plus grandes que le temps qui sépare deux collisions d’une molécule (environ 10-11 s).

Le raisonnement précédent s’applique aussi lorsque, au lieu d’être matérialisé par une paroi, le plan z = 0 est une interface entre deux couches fluides dont l’une est en mouvement dans son propre plan, à la vitesse u, entre le fluide situé au-dessus d’elle et le fluide situé au-dessous. La loi de Newton permet donc d’exprimer la force tangentielle, souvent appelée le frottement, que les couches fluides exercent les unes sur les autres. Cette force tangentielle, orientée dans la direction de la vitesse, s’ajoute à la force de pression qui, elle, est orientée suivant la normale à l’interface (Lire Pression, température et chaleur).
7. Le mécanisme de la diffusion dans les liquides
Le fait que tout liquide ait un volume propre implique que les molécules qui le compose sont proches les unes des autres. La distance moyenne entre molécules voisines dépend de la pression exercée sur ce liquide ; dans les conditions normales (p ≈ 103 hPa) elle est légèrement supérieure à la taille des molécules, typiquement 10-10 à 10-9 m. L’agitation thermique de toutes ces molécules, que l’on peut comparer à une vibration, confère à ce milieu liquide une certaine diffusivité, mais celle-ci est beaucoup plus faible que celles des gaz. La différence tient essentiellement au fait que, dans un liquide, le rayon d’action d’une molécule est inférieur à sa taille, alors que, dans un gaz, c’est le libre parcours moyen, environ 25 fois la taille des molécules. Cette faiblesse explique que, pour bien dissoudre le sucre dans une tasse de café, il soit nécessaire d’ajouter un brassage macroscopique en remuant l’ensemble avec une cuiller.
Toute particule possédant une différence par rapport aux molécules et présente dans ce milieu est constamment soumise aux vibrations de l’ensemble. Un bilan analogue à celui fait pour les gaz en section 3 met nécessairement en évidence un débit net de ces particules, du côté le plus riche vers le plus pauvre. Ce débit peut encore s’écrire avec la loi de Fick : φ = -D dC/dx, où D désigne la diffusivité des particules dans le liquide et C leur concentration volumique.
Pour prédire la diffusivité massique d’un liquide, qui traduit son aptitude à transporter une autre espèce matérielle, on dispose de la loi suivante proposée par Einstein en 1905 [11] : D = kBT/6πμr, où kB = 1,38×10-23 J.K-1, est la constante de Boltzmann, T la température absolue, μ la viscosité dynamique du liquide et r le rayon de la particule transportée. Avec r ≈ 10-9 m, dans un liquide comme l’eau où μ ≈ 10-3 Pa.s, à la température ambiante proche de 300 K, on obtient D ≈ 2×10-10 m2.s-1, valeur environ 10 000 fois plus faible que la diffusivité d’un gaz. Dans la formule d’Einstein, on remarquera que T intervient au numérateur, ce qui traduit bien le fait que l’agitation thermique est le vrai moteur de la diffusion. Et le fait que μ et r interviennent au dénominateur signifie que la viscosité s’oppose à la diffusion et que plus les particules sont grosses, plus difficile est leur diffusion.
Pour l’eau et pour tout liquide électriquement isolant, la chaleur et la masse ont des diffusivités voisines. Par contre pour des métaux liquides, la conduction électronique constitue un autre mécanisme de transport de la chaleur, qui peut se révéler beaucoup plus important que la diffusivité massique. L’exemple le plus connu est celui du sodium liquide, utilisé pour refroidir les réacteurs nucléaires du type surrégénérateur comme Phénix, en fonctionnement à Marcoule de 1973 à 2010. Sa diffusivité thermique à une température voisine de 300 K est de l’ordre de 7×10-5 m2.s-1, plus de 10 000 fois supérieure à sa diffusivité massique.
8. Messages à retenir
- La diffusion d’une espèce particulière au sein d’un mélange, tout comme la diffusion de la chaleur et celle de la quantité de mouvement, résultent de l’agitation des particules élémentaires, molécules ou atomes. C’est un mécanisme de transport très lent, mais sans compétiteur aux échelles microscopiques.
- Dans les fluides comme l’air et l’eau, peu visqueux, la turbulence parvient à disperser les polluants, la chaleur et la quantité de mouvement. Mais ce mécanisme ne peut pas atteindre des échelles inférieures à celles des plus petits tourbillons, contrôlée par la viscosité, en général supérieure au micron. La diffusion moléculaire la relaie pour achever le mélange.
- Les lois de la diffusion ont d’abord été découvertes empiriquement avant de faire l’objet de modèles théoriques. Relativement simple dans le cas des gaz dilués comme l’air, celui-ci a pu être esquissé dans cet article. Son équivalent dans le cas des liquides est beaucoup plus complexe et fait encore l’objet de recherches.
Références et notes
Image de couverture. Avant le lever du soleil, en pleine campagne, dans l’air encore immobile, c’est par diffusion que les contaminants relâchés par la végétation sont transportés dans l’air. [Source : pixabay, libre de droits].
[1] Un nanomètre vaut un milliardième de mètre (10-9 m), un micromètre, ou micron, vaut un millionième de mètre (1 μm = 10-6 m).
[2] Ludwig Boltzmann (1844-1906), physicien et philosophe autrichien, a introduit ce modèle moléculaire dit des « sphères dures » qui conduit à une célèbre équation portant son nom.
[3] Il est fréquent de lui substituer la viscosité cinématique ν, qui est le quotient entre la viscosité μ et la masse volumique ρ, soit ν = μ/ρ.
[4] Toutes ces vitesses, avec leurs orientations et leurs valeurs respectives, peuvent être représentées à l’aide de la fonction de distribution de Maxwell. Leur prise en compte conduirait à de longs calculs hors de portée de cet article.
[5] Cette expression est plus connue sous la forme kBT = mc2/3, en introduisant la constante de Boltzmann kB, reliée à R et au nombre d’Avogadro NA = 6,0248 × 1023, par kB = R/NA= 1,380 × 10-23 J/K (joule par Kelvin).
[6] Par exemple, à l’aube, dès que l’ensoleillement commence à réchauffer le sol, par diffusion celui-ci réchauffe les couches d’air les plus basses, qui deviennent plus légères que celles situées au-dessus d’elles. Cette situation où le fluide lourd est situé au-dessus du fluide léger est instable.
[7] Ludwig Prandtl (1875-1953) était un physicien allemand, professeur à l’université de Munich, qui a apporté d’importantes contributions à la mécanique des fluides. On lui doit notamment les idées fondatrices de la théorie de la couche limite, le concept de longueur de mélange et une théorie simple pour calculer la portance d’une aile d’envergure finie.
[8] M. Lesieur, Turbulence, EDP Sciences, collection Grenoble sciences, 2013, p. 128.
[9] La propriété que φ = -τ peut être établie en écrivant l’équilibre global d’un petit domaine gazeux situé du côté z>0 de la paroi qui exerce sur le fluide la force tangentielle –τ. L’expression de cet équilibre global est souvent appelée théorème des quantités de mouvement.
[10] L’établissement de cette expression est en réalité dû à Navier, congénère de Fourier (voir le focus Les pères du concept de diffusion).
[11] Albert Einstein, Investigations on the Theory of the Brownian Movement, Dover Publications, Inc. (1985), (ISBN 0-486-60304-0). Réédition des articles originaux d’Einstein sur la théorie du mouvement brownien
L’Encyclopédie de l’environnement est publiée par l’Association des Encyclopédies de l’Environnement et de l’Énergie (www.a3e.fr), contractuellement liée à l’université Grenoble Alpes et à Grenoble INP, et parrainée par l’Académie des sciences.
Pour citer cet article : MOREAU René (19 septembre 2018), La diffusion, étape ultime d’un bon mélange, Encyclopédie de l’Environnement. Consulté le 29 mars 2025 [en ligne ISSN 2555-0950] url : https://www.encyclopedie-environnement.org/physique/diffusion-etape-ultime-bon-melange/.
Les articles de l’Encyclopédie de l'environnement sont mis à disposition selon les termes de la licence Creative Commons BY-NC-SA qui autorise la reproduction sous réserve de : citer la source, ne pas en faire une utilisation commerciale, partager des conditions initiales à l’identique, reproduire à chaque réutilisation ou distribution la mention de cette licence Creative Commons BY-NC-SA.