Les lois de la dynamique

La loi de Newton reliant force et accélération est à l’origine de la physique moderne. Appliquée à chaque parcelle de fluide, elle est au cœur des modèles de prévision météorologique et climatique. La notion intuitive de force est utilisée depuis l’antiquité pour comprendre les équilibres statiques. Elle permet de concevoir les voutes en architecture, d’utiliser un levier, de décrire l’équilibre des fluides sous l’effet de la poussée d’Archimède. C’est le principe d’inertie découvert par Galilée qui a ouvert la voie aux lois de la dynamique de Newton, dont le grand succès a été d’expliquer le mouvement des planètes et satellites, ainsi que les marées. Ceci a nécessité une grande expertise mathématique, qui trouve ses limites pour des systèmes plus complexes comme l’atmosphère ou l’océan. La résolution des équations de la dynamique n’a été alors possible que depuis l’avènement  du calcul informatique. Cependant les lois de conservation, quantité de mouvement, énergie, le moment cinétique, apportent des contraintes globales permettant une compréhension plus directe de certains phénomènes.

1. Forces à l’équilibre

La notion de force exprime une action mécanique sur un objet. Les forces ont une origine physique bien identifiée, par exemple la force de gravitation (le poids), la force électrique sur une particule chargée, la force de contact ou de tension sur un câble, ou la force élastique d’un ressort. Comme beaucoup de notions fondamentales de physique, la force est difficile à définir en soi, mais elle s’appréhende par des exemples expérimentaux ainsi que par les relations mathématiques qu’elle possède avec d’autres quantités.

Une force est ainsi caractérisée par son intensité (ou module) et sa direction, ainsi que son point d’application, et se représente mathématiquement par un vecteur. La somme des forces agissant sur un objet au repos doit s’annuler. On peut mesurer une force par l’élongation d’un ressort par rapport à sa position de repos (Figure 1). On vérifie expérimentalement que cet allongement est proportionnel à la force en ajoutant successivement plusieurs poids identiques. Une fois étalonné, ce dynamomètre à ressort peut être utilisé pour mesurer différentes forces.

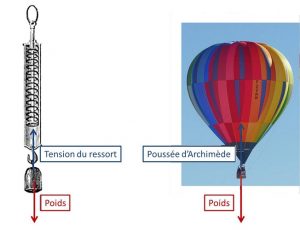
Pour une montgolfière immobile dans l’air, le poids total est équilibré par la poussée d’Archimède, égale et opposée à la masse du volume d’air déplacé. Celle-ci n’est autre que la résultante des forces de pression atmosphérique agissant tout autour de  l’enveloppe : en raison de la diminution de pression avec l’altitude, la pression est plus forte en bas de  l’enveloppe qu’en haut, ce qui se traduit en une force nette vers le haut. Cet équilibre entre pression et force de gravité s’applique en fait à tout volume de fluide en équilibre, ce qu’on appelle l’équilibre hydrostatique (lire « Pression, température, chaleur »). C’est grâce à cet équilibre que les parcelles d’air, ou les parcelles d’eau au sein d’un bassin, ne tombent pas vers le sol sous l’effet de la gravité. Lorsque l’air est chauffé, sa densité et donc la masse d’un volume donné diminuent, tandis que la pression reste inchangée, car contrôlée par le poids de l’air environnant. L’équilibre est alors rompu conduisant à une accélération verticale de la montgolfière. Dans l’atmosphère une masse d’air chauffée localement par le rayonnement solaire aura de même tendance à s’élever : c’est le principe de la convection.

De façon plus générale, l’équilibre des forces doit s’exprimer sous forme de vecteurs, ce qui est à la base du calcul des structures en architecture, voir Figure 2. Pour chaque point matériel, par exemple le nœud d’intersection des fils, la somme vectorielle des forces doit s’annuler à l’équilibre, comme il est représenté sur la Figure 3a. Ceci permet par exemple de trouver les intensités des forces F₁ et F₂ connaissant la force F₃ et les angles θ₁ et θ₂, soit par construction géométrique, soit numériquement en projetant les vecteurs selon les axes verticaux et horizontaux.

Un objet étendu, par exemple un solide, est décrit en physique comme un ensemble de points matériels maintenus en cohésion par des forces internes.  Ces forces sont à distinguer des forces externes comme le poids ou les forces de contact avec d’autres objets. La somme des forces internes s’annule par le principe de l’action et de la réaction, de sorte que l’équilibre impose l’annulation de la somme  des forces externes.

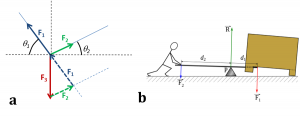
Mais la condition d’équilibre d’un objet étendu impose aussi l’annulation du moment total des forces, pour éviter sa mise en rotation. Le moment d’une force par rapport à un axe est défini comme le produit de la force, projetée perpendiculairement à l’axe, par la distance à l’axe. L’exemple classique est le levier représenté sur la Figure 3b. A l’équilibre, ou quasi-équilibre pour un mouvement lent, l’annulation des moments impose que F₁d₁ = F₂d₂ (les forces étant ici perpendiculaires à l’axe) ce qui permet d’amplifier la force exercée dans le rapport inverse des distances à l’axe (selon la convention habituelle on note ici F₁ l’intensité de la force tandis que F₁ représente le vecteur force).

Il est habituel de considérer les moments par rapport à l’axe du levier, car le moment de la force de réaction R du sol s’y annule. On pourrait cependant obtenir le même résultat en calculant le moment par rapport à n’importe quel axe mathématique, en ajoutant le moment de la réaction R, vecteur égal et opposé à la somme des deux forces F₁ et F₂.

2. Forces et accélération

Quittant maintenant le domaine de la statique, l’accélération d’un objet est liée à  la force totale F qui agit dessus par la fameuse loi de la dynamique de Newton, F = mg où m est la masse de l’objet et g son vecteur accélération. Ceci permet de définir l’unité de force, le Newton (N), comme la force produisant une accélération de 1 (m/s)/s sur une masse de 1kg, ce qu’on écrit  1 N = 1 kg m s^-2.

En l’absence de force, un objet se déplace donc à vitesse uniforme, c’est le principe d’inertie énoncé en premier par Galilée (1564-1642). Ce principe était peu intuitif à l’époque, car dans la vie courante tout mouvement tend à cesser en l’absence d’effort.  Ce ralentissement (accélération négative) est maintenant attribué aux forces de frottement, opposées à la vitesse. Mais le frottement devient négligeable dans le vide interplanétaire, et le grand succès de Newton (1643-1727) a été de décrire mathématiquement le mouvement des planètes et satellites à partir d’une loi simple de force d’attraction universelle décroissant comme l’inverse du carré de la distance r.

L’application de la loi de Newton a nécessité l’invention du concept mathématique de dérivée précisant les notions de vitesse et d’accélération. On note ainsi la vitesse v = dz/dt où dz est un petit déplacement en un intervalle de temps dt. On considère en fait la limite d’un intervalle de temps très court. De façon similaire l’accélération est notée g = dv/dt. Pour une accélération g constante, la vitesse est proportionnelle au temps, v = gt, et on démontre facilement que la distance de chute (différence entre altitude initiale z₀ et altitude z) est alors  z₀–z = (1/2) gt². Ainsi sur Terre sous l’action de la pesanteur, g = 9,8 m s^-2, un objet atteint en 1s une vitesse 9,8 m/s (35 km/h), et chute d’une hauteur de 4,9 m.

La loi de Newton s’applique plus généralement sous forme vectorielle : l’objet peut chuter selon la verticale comme énoncé précédemment tout en conservant sa composante de vitesse horizontale par inertie. Pour une vitesse horizontale suffisamment grande la courbure de la Terre doit alors être prise en compte, et on obtient le mouvement circulaire d’un satellite, voir Figure 4. Dans ce cas la vitesse est constante en module mais le vecteur vitesse tourne à la même vitesse angulaire [1] que le satellite. L’accélération est alors perpendiculaire à la vitesse et dirigée vers le centre de la Terre, avec la valeur g = v²/r, comme montré sur la Figure 4. Ainsi pour un satellite proche [2] de la Terre, g = 9,8 ms^-2, r = 6500 km, ce qui conduit  à la vitesse v = (gr)^1/2 = 8 km/s, un temps de révolution (longueur 40 000 km) T = 5000 s (1 h 23 min).

Si maintenant la gravité g décroit en 1/r², la vitesse v = (gr)^1/2 du mouvement circulaire décroît en 1/r^1/2 et la période de révolution, égale à 2πr/v, croit en r^3/2.  Ainsi la Lune distante de la Terre de  r = 384 000 km, soit 60 fois le rayon terrestre,  doit tourner en un temps 465 fois plus long qu’un satellite proche, soit 27 jours. Ceci est conforme aux observations [3]. La loi de croissance du temps de révolution en r^3/2 avait été découverte par Kepler (1571-1630) pour les planètes en orbite autour du Soleil.  Au-delà du cas particulier de l’orbite circulaire, Newton a pu démontrer que le mouvement général suit une ellipse (ou une hyperbole au-delà de la vitesse d’échappement), et il a pu retrouver les trois lois antérieurement établies par Kepler à partir de mesures précises des positions des planètes.

Il se trouve que la force de gravité est elle-même proportionnelle à la masse, de sorte que l’accélération produite en est indépendante : tous les corps tombent avec la même accélération en un même lieu. Cette équivalence entre masse pesante et masse inertielle a été énoncée par Galilée, et illustrée par ses fameuses expériences (peut-être seulement imaginées) de chute d’objets de la Tour de Pise. Ceci a été refait avec grande précision dans le vide,  évitant ainsi le frottement de l’air. A titre de démonstration pour le public, un film comparant la chute d’un marteau et d’une plume a été réalisé sur la Lune lors de la mission Apollo XV [4], et une expérience similaire filmée sur Terre dans une immense chambre à vide [5]. C’est à cause de ce principe d’équivalence que tous les objets flottent en apesanteur dans un satellite, chacun suivant exactement la même orbite autour de la Terre. Cette équivalence est maintenant testée avec une précision relative de 10^-13 (1/10 000 milliards), et une précision de 10^-15 est attendue du satellite « Microscope » lancé récemment. Ces mesures ultra-précises visent à tester des écarts au principe d’équivalence prédites par de nouvelles théories de la gravitation.

3. Energie cinétique et potentielle

Dans l’exemple de la chute libre évoqué plus haut, on peut noter que mg(z₀-z) = m(1/2)g²t² = (1/2)mv².  Ceci correspond à la propriété plus générale de la conservation de l’énergie totale, composée de l’énergie cinétique (1/2)mv² et de l’énergie potentielle mgz. Lorsqu’un objet chute son énergie cinétique augmente, mais son énergie potentielle diminue d’autant, de sorte que l’énergie mécanique totale est conservée (en l’absence de frottement). Dans le cas général l’énergie cinétique (1/2)mv² s’exprime en fonction du module de la vitesse. La conservation de l’énergie mécanique se généralise au cas d’un satellite mais l’expression de l’énergie potentielle doit alors être modifiée pour tenir compte de la décroissance de la force de gravité. Cette énergie potentielle ne dépend que de la position de l’objet, de sorte qu’elle retrouve la même valeur après une révolution, et l’énergie cinétique elle aussi retrouve la même valeur, en accord avec le fait que le mouvement planétaire persiste indéfiniment. On définit le potentiel de gravité en divisant cette énergie potentielle par la masse de l’objet. Ce potentiel caractérise le champ de gravité indépendamment de l’objet qui gravite autour (tant que l’objet est petit et ne met pas la planète en mouvement par réaction).

La conservation de l’énergie mécanique suppose une forme particulière des lois de force. Les forces de frottement, contrairement à la gravité, font diminuer l’énergie mécanique, de sorte qu’un satellite finit par tomber au contact de l’atmosphère résiduelle. L’énergie mécanique perdue est cependant convertie en chaleur de sorte que l’énergie totale reste conservée (lire « L’énergie »). La chaleur correspond essentiellement à l’énergie cinétique désordonnée des molécules du gaz.

Pour une planète sphérique homogène, le potentiel varie en -1/r, de sorte que les équipotentielles sont des sphères concentriques. Cependant ces sphères sont légèrement déformées à cause de la rotation terrestre et des inhomogénéités de la Terre. La forme d’équilibre de la surface océanique est une telle équipotentielle (lire « Le milieu marin »). En effet un objet se déplaçant sur une équipotentielle conserve la même énergie potentielle, et comme son énergie totale est conservée, il ne peut pas acquérir (ni perdre) de vitesse sous l’effet de la seule gravité. Inversement si la forme de l’océan s’écarte d’une équipotentielle, l’eau de surface a tendance à s’écouler vers les régions de plus faible potentiel jusqu’à les combler et atteindre l’état d’équilibre où la surface est une équipotentielle. La surface de la Terre solide se rapproche également d’une équipotentielle sous l’effet de l’érosion et de la plasticité du manteau terrestre.

4. Quantité de mouvement

La quantité d’un mouvement d’une masse élémentaire (considérée comme ponctuelle) est définie comme le produit de la masse par la vitesse, définition qu’on peut étendre à tout système physique en ajoutant (vectoriellement) les quantités de mouvement de chacune de ses  masses élémentaires. On démontre facilement que la quantité de mouvement est égale à la quantité de mouvement du centre d’inertie (barycentre) du système affecté de sa masse totale. La loi de la dynamique de Newton indique alors que la dérivée temporelle de la quantité de mouvement est égale à la somme des forces agissant sur le système.

Selon un principe fondamental de la physique, la quantité de mouvement d’un système isolé est conservée. Autrement dit son centre d’inertie se déplace en translation à vitesse uniforme, et seules les forces externes peuvent modifier cette vitesse. Une autre formulation équivalente est le principe de l’action et de la réaction qui stipule que tout corps A exerçant une force sur un corps B subit une force d’intensité égale, mais de sens opposé, exercée par le corps B. La loi de la dynamique indique alors que ces forces internes ne changent pas la quantité de mouvement du système global A+B. Ceci généralise la condition d’équilibre statique discutée plus haut.

Cette loi est utilisée notamment pour étudier les chocs, comme illustré sur la Figure 5. Connaissant les masses m₁ et m₂ et vitesses initiales u₁ et u₂ de chaque masse, on calcule la quantité de mouvement avant le choc m₁u₁+m₂u₂, qui doit être préservée après le choc, apportant ainsi une contrainte sur les vitesses finales. Si on suppose de plus que le choc est élastique, c’est-à-dire que l’énergie cinétique (1/2)m₁u₁²+(1/2)m₂u₂² est conservée, on peut déduire les deux vitesses finales. Pour deux masses égales, on a ainsi un échange des vitesses (Figure 5a). Dans le  cas d’un choc complètement inélastique, les masses restent liées après le choc, avec une vitesse finale égale à la moyenne pondérée des vitesses initiales  m₁u₁+m₂u₂/(m₁+m₂)  par conservation de la quantité de mouvement. Appliquées aux molécules d’un gaz, ces propriétés des chocs permettent d’interpréter le phénomène de viscosité qui égalise les quantités de mouvements des zones rapides et lentes au sein du fluide, en préservant la quantité de mouvement totale.

La propulsion des fusées ou des avions constitue un autre exemple classique : la quantité de mouvement apportée au véhicule étant juste opposée à celle du gaz éjecté, indépendamment des mécanismes complexes mis en jeu. Cela s’applique aussi aux forces de gravité, la Lune attirant la Terre avec une  force égale et opposée à la force de gravité Terrestre agissant sur la Lune. La Terre tourne ainsi autour du centre d’inertie du système Terre-Lune à la manière du lanceur de marteau qui doit tourner pour compenser la réaction du boulet en rotation (lire « Les marées »). C’est ce centre d’inertie qui décrit l’orbite elliptique autour du Soleil et non la Terre elle-même.

 

5. Moment cinétique

Le moment cinétique par rapport à un axe est défini pour une masse ponctuelle comme le produit de la distance à l’axe par sa quantité de mouvement projetée perpendiculairement à cet axe. Cette définition se généralise à un corps étendu, par exemple un solide, en le scindant par la pensée en masses élémentaires, et en ajoutant leurs moments cinétiques. On démontre à partir de la loi de la dynamique que la dérivée temporelle du moment cinétique est égale au moment total des forces (encore appelé « couple ») agissant sur le système. Ceci généralise la loi de la statique qui impose que le moment total des forces soit nul.

La loi de conservation du moment cinétique stipule que le moment total des forces internes s’annule, et donc seul le moment des forces externes peut changer le moment cinétique. Ainsi dans un solide les forces internes de cohésion n’interviennent pas dans le bilan de moment cinétique, de même qu’elles n’interviennent pas dans la quantité de mouvement. Il s’agit d’une loi fondamentale de la physique, distincte et complémentaire du principe de l’action et de la réaction.

Autrement dit un système ne peut pas se mettre à tourner spontanément  ni perdre sa rotation initiale sans l’action de forces externes. Sa vitesse de rotation peut cependant changer en cas de contraction ou d’extension. En effet pour une masse ponctuelle, c’est le produit ur de la vitesse u par la distance r à l’axe qui est conservé, donc la vitesse u croît en proportion inverse de la distance r, et sa vitesse angulaire u/r en proportion inverse du carré de cette distance.

L’exemple classique est celui de la patineuse, et dans les milieux naturels, la formation de tornades et cyclones (lire « Les tornades : de puissants tourbillons dévastateurs »). La rotation de la Terre elle-même résulte de l’amplification de la vitesse angulaire pendant  l’accrétion de la matière ayant conduit à sa formation. L’exemple le plus spectaculaire est celui des pulsars, étoiles extrêmement denses tournant avec une période de quelques secondes à quelques millisecondes. Ces objets résultent de l’effondrement d’une étoile massive, passant ainsi typiquement d’un rayon de 1 million de km à 10 km. Une telle contraction augmente la vitesse angulaire de rotation d’un facteur 10 milliards (une partie du moment cinétique étant cependant éjectée avec le gaz émis par l’explosion).

Le moment cinétique est en fait un vecteur, aligné avec l’axe de rotation[6], et il se conserve donc aussi bien en direction qu’en module. C’est le principe du gyroscope. De même l’axe de rotation terrestre reste aligné par rapport aux étoiles, le pôle Nord restant pointé vers une région proche de l’Etoile polaire.

Ceci n’est vrai que pour un système isolé, et plus précisément en l’absence de couple (ou moment) des forces extérieures. Un couple perpendiculaire à l’axe de rotation produit une rotation de l’axe de rotation, sans changement de la vitesse angulaire : c’est le phénomène de précession qu’on observe sur une toupie, voir Figure 6 (de même qu’une accélération perpendiculaire à la vitesse produit une rotation de la vitesse sans changement de son module). Un effet similaire se produit pour la Terre en raison de sa forme aplatie au pôle : un couple résulte de l’attraction lunaire plus forte sur la partie proche du bourrelet que sur sa partie  opposée. Ceci conduit à un lent mouvement de précession de la rotation terrestre en une période de 26 000 ans (cf. Figure 6). Ainsi la  direction du pôle se déplace lentement sur la sphère céleste au cours des siècles. Il en résulte un déplacement sur l’orbite terrestre de la position des équinoxes, moment où l’axe de rotation terrestre est orienté perpendiculairement à la direction du Soleil. C’est pourquoi le phénomène est appelé « précession des équinoxes ». La variation d’ensoleillement associée intervient dans les changements climatiques entre périodes glaciaires et tempérées.

 

---

Références et notes

Photo de couverture : By 极博双板滑雪俱乐部 (Uploaded to Flickr as jfpds regular) [CC BY-SA 2.0 (http://creativecommons.org/licenses/by-sa/2.0)], via Wikimedia Commons

[1] La vitesse angulaire Ω est l’angle parcouru par unité de temps, exprimé généralement en radian/s, de sorte que Ω=v/r . Un radian est défini comme l’angle interceptant un arc de cercle égal au rayon, de sorte que le tour complet (circonférence 2πr) représente 2π radian, et la période de révolution est T=2π/Ω=2πr/v.

[2] L’altitude doit être de quelques centaines de km pour éviter la friction atmosphérique, mais l’accélération de la gravité y reste proche de celle de la surface terrestre, et le rayon de l’orbite est peu différent  de celui de la Terre.

[3] Il s’agit ici de la révolution sidérale, c’est-à-dire par rapport aux étoiles, tandis que le temps entre deux pleines Lunes, de 29,5 jours, est la révolution synodique, c’est-à-dire par rapport au Soleil.

[4] Apollo 15 Hammer and Feather Drop- Youtube

[5] Brian Cox visits the world’s biggest vacuum chamber – Human Universe: Episode 4 Preview – BBC Two – Youtube

[6] Le moment cinétique est plus précisément défini par rapport à un point origine O. Pour une masse ponctuelle m au point M c’est le produit vectoriel du vecteur OM par la quantité de mouvement mu de la masse au point M. Pour un solide axisymétrique comme une toupie ou la Terre, le moment cinétique est aligné sur l’axe de rotation, avec une valeur proportionnelle à la vitesse angulaire et au moment d’inertie.