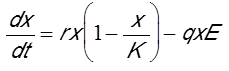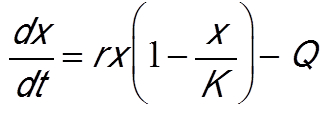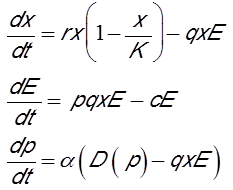Les modèles mathématiques peuvent aider à mieux gérer la pêche

La pêche fournit une part importante de la nourriture des populations dans certains pays en développement. Ceci peut induire une cascade préoccupante : surpêche, effondrement des captures et augmentation des prix sur les marchés, extinction de nombreuses espèces. Comment éviter que cette situation devienne catastrophique et, au contraire, la stabiliser ? La modélisation mathématique, en couplant les dynamiques écologiques et économiques, permet de mieux comprendre la dynamique des systèmes de pêcheries. Elle est présentée ici de façon élémentaire et illustrée par le cas particulier du thiof, une espèce emblématique menacée au Sénégal.

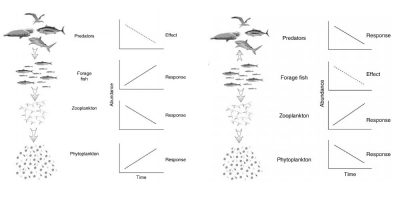
1. Interactions trophiques au sein des écosystèmes marins

Un élément particulièrement structurant des écosystèmes marins est que les interactions trophiques dépendent de la taille des individus [1] : les grands poissons mangent les petits (Figure 1). De ce fait, une exploitation ciblant les espèces de grande taille, ou les espèces de petite taille, aura des effets en cascade différents sur l’ensemble des niveaux trophiques d’un écosystème marin. De façon schématique, dans le premier cas, la diminution de l’abondance d’espèces de grande taille, telles que les thons, entraîne l’augmentation de l’abondance des espèces de plus petite taille dont les thons se nourrissent, comme les sardines. Cette augmentation entraîne elle-même la diminution d’espèces dont les sardines se nourrissent, telles que le zooplancton, et finalement l’augmentation des proies du zooplancton, le phytoplancton (Figure 2, partie de gauche) [2].

Dans le second cas où la pêche cible directement les sardines, la diminution de leur abondance entraîne à la fois la diminution des thons et l’augmentation du zooplancton, celle-ci entraînant la diminution du phytoplancton (Figure 2, partie de droite). Dans cette vision simplifiée, la stratégie serait d’exploiter les espèces de taille, et donc de niveau trophique, de plus en plus petit, conduisant au phénomène « fishing down the food web » [3]. Dans la réalité, les réseaux trophiques sont plus complexes mais il existe de nombreux exemples corroborant ce schéma d’une exploitation d’espèces situées vers le haut de la chaîne alimentaire ayant conduit au bouleversement de la structure et du fonctionnement d’écosystèmes marins (Figure 3) [4].

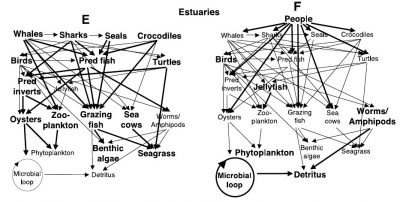
2. Bases de l’économie de la pêche

En théorie, l’exploitation d’une espèce peut conduire à son extinction si son prix augmente plus vite que le coût de son exploitation lorsque le niveau d’abondance diminue [5], ou si son aire de distribution se contracte sous l’effet de l’exploitation, sans augmentation significative de coût [6]. Dans les faits, si les extinctions globales d’espèces marines sont rares, leur extinction locale, ou la disparition de leur rôle écologique ou économique, ne l’est pas [7]. Pour parvenir à une exploitation écologiquement et économiquement durable des ressources marines, l’application de mesures de gestion des pêcheries selon une approche pluridisciplinaire [8] et écosystémique [9] est la voie recommandée. La spatialisation du milieu marin et de ses usages, dont la pêche, constitue un enjeu majeur. Il s’agit en particulier que les zonages économiques, telles que les zones économiques exclusives, et les espaces dédiés à la conservation, comme les aires marines protégées, soient écologiquement cohérents.

Une grande partie des espèces de poissons commerciales sont surexploitées. Les principales espèces concernées par la surpêche sont la morue à Terre-Neuve, la sardine en Californie, l’anchois du Pérou, le hareng en mer du Nord ou encore l’espèce Epinephelus aeneus plus connue sous le nom de « thiof » le long de la côte atlantique de l’Afrique occidentale. Ce mérou est appelé thiof au Sénégal, mot emprunté au vocabulaire lébou et wolof. Le thiof était utilisé traditionnellement dans la préparation du plat national sénégalais, le thiep bou dien, composé de poisson, de légumes variés et de riz. Les captures du thiof n’ont fait que diminuer au Sénégal jusqu’en 2006 (données du CRODT [10], Figure 4).

La pêche est essentielle pour l’économie de nombreux pays en développement. Les espèces commerciales locales sont exploitées par des flottes de pêche artisanale (Figure 5A). L’exploitation intensive est également réalisée par la pêche industrielle en vertu d’accords de pêche avec les gouvernements des pays en développement (Figure 5B). Les poissons sont une source importante de nourriture pour les populations locales. Lorsque les captures s’effondrent du fait de la surpêche, les prix de vente sur le marché augmentent, ce qui rend l’accessibilité de la ressource de plus en plus difficile pour les populations les plus pauvres.

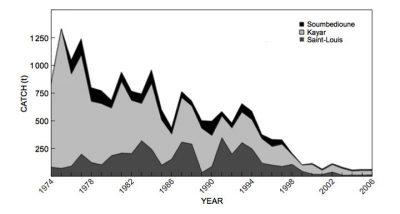
3. Un modèle mathématique simple d’évolution de la biomasse d’une espèce exploitée

Il est donc important de comprendre les mécanismes qui gouvernent la dynamique des pêcheries commerciales. Une gestion des ressources marines doit s’appuyer sur des outils d’aide à la décision permettant aux gestionnaires et aux décideurs de prendre des mesures de conservation et d’exploitation optimale des pêcheries. La modélisation mathématique permet de développer de tels outils dans le but de prévoir les effets des aménagements du littoral et des mesures de contrôle de la pêche.

Les modèles mathématiques dans le domaine des pêches sont basés sur des hypothèses concernant les mécanismes de production et d’extinction des espèces exploitées.

Nous allons maintenant présenter un modèle classique qui ne comporte qu’une seule inconnue x(t), la biomasse de l’espèce exploitée, dépendant de la variable temps t. Le membre de gauche de l’équation est la dérivée de la biomasse en fonction du temps (dx/dt). Il représente la vitesse de variation de la biomasse. Le membre de droite de l’équation comporte deux termes, un terme de production de biomasse et un terme d’extinction. Le terme de production représente la croissance de la biomasse du stock de poissons. Le terme d’extinction correspond à la capture par la pêche. Ces deux termes font intervenir des paramètres (r, K, q, E) qui sont des constantes. Pour les espèces de poissons commerciales, il est habituel de choisir pour le terme de production la loi de croissance logistique qui a été testée sur de nombreuses espèces animales. Le paramètre r représente le taux de croissance de la population de poissons.

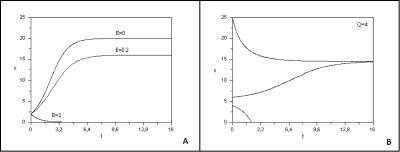
Lorsque la biomasse est très faible, la croissance logistique est exponentielle. Lorsque la biomasse devient plus importante, résultant de la compétition intra-spécifique pour les ressources, la croissance est freinée pour atteindre une valeur d’équilibre K, appelée capacité limite, pour laquelle la production s’annule, comme le montre la Figure 6A (courbe avec E=0).

La capacité limite représente donc la biomasse d’équilibre vers laquelle tendrait le stock en absence de pêche. Le second terme négatif du second membre de l’équation ci-dessous représente la capture par la pêche avec un taux de capture q appelé « capturabilité ». Il est habituel dans le domaine des pêches de faire l’hypothèse que la capture est proportionnelle au produit de la biomasse de la ressource par l’effort de pêche E. Cet effort de pêche représente l’investissement dans la pêche. Il est proportionnel au nombre de navires de la flotte, ou bien il s’obtient par le calcul du nombre d’heures de pêche en mer. Avec ces hypothèses, le modèle s’écrit :

La Figure 6A [11] illustre les résultats du modèle en montrant l’évolution au cours du temps de la biomasse totale de poissons pour différents efforts de pêche.

Ce modèle très simple, avec un effort de pêche maintenu à un niveau constant, prédit deux cas [12] :

• si l’effort de pêche est trop élevé (qE>r), la ressource va à l’extinction. Dans ce cas, la pêche a un taux de prélèvement plus grand que le taux de reproduction du poisson, qui disparaît (Figure 6A avec E =2).
• si la pression de pêche est modérée (qE<r), la ressource va tendre à long terme vers un équilibre de biomasse positif inférieur à la capacité limite K et qui est globalement stable (Figure 6A avec E = 0.2).

Dans le cas où la ressource se maintient malgré l’exploitation, il est de plus possible de choisir un « bon » effort de pêche permettant d’optimiser la capture à l’équilibre. Cet optimum correspond au Rendement Maximal Durable (RMD, en anglais « Maximum Sustainable Yield », MSY). Dans notre cas, le « RMD » est atteint lorsque l’effort de pêche est choisi égal à la moitié du taux de croissance de l’espèce exploitée (qE = r/2). Une abondante littérature existe sur ce sujet notamment en utilisant des méthodes du contrôle optimal [13]. On dit qu’une espèce est surexploitée lorsque l’effort de pêche est maintenu à un niveau supérieur à celui du RMD. On parle de surpêche lorsque la proportion de poissons reproducteurs devient trop faible pour assurer le renouvellement de l’espèce et menace sa survie.

Un autre mode d’exploitation consiste à fixer un quota de pêche. Le modèle précédent, en supposant une capture avec quota constant représenté par le paramètre Q, devient (Beddington et May [14]) :

L’étude de ce modèle montre qu’un quota même faible peut générer un effet « Allee », c’est-à-dire qu’en dessous d’un seuil, la population va rapidement à l’extinction. La Figure 6B [11] montre l’évolution au cours du temps de la biomasse de la ressource pour différentes conditions initiales. Avec une condition initiale choisie au-dessous d’un seuil, la population disparaît. La grande variabilité des conditions environnementales en milieu marin d’une année à l’autre peut justement induire un passage en dessous d’un seuil et conduire irrémédiablement l’espèce exploitée à l’extinction. Dans les années 1970, la pêche à la baleine était autorisée librement avec pour effet de provoquer une chute très importante de ses effectifs. Ces modèles mathématiques ont permis d’alerter les décideurs sur les risques d’une pêche avec quota fixe.

4. La prise en compte des aspects économiques : les modèles bioéconomiques

Il est également crucial de prendre en compte dans les modèles de gestion des pêcheries les aspects économiques, et tout particulièrement les variations de l’investissement et du prix. Le modèle comporte alors trois variables : la biomasse de la ressource x, l’effort de pêche E et le prix p de la ressource sur le marché [15]. La première équation est la même que celle du premier modèle présenté. La deuxième équation décrit la variation de l’investissement. L’effort de pêche augmente si la pêcherie est rentable et inversement. Ainsi, la seconde équation fait la différence entre le bénéfice net de la pêcherie, correspondant à la capture multipliée par le prix, diminué des coûts d’exploitation de la pêcherie. Les coûts c par unité d’effort de pêche résultent de l’achat du fuel, des salaires des pêcheurs et des différentes taxes. La troisième équation donne la variation du prix de la ressource sous l’effet de l’offre et de la demande. L’offre est représentée par la capture instantanée et la demande est représentée par une fonction D(p) monotone décroissante du prix. En d’autres termes, si le prix augmente, la demande diminue, et vice-versa. Sous ces hypothèses, le modèle s’écrit :

Les deux premières équations correspondent au modèle prédateur-proie de Lotka-Volterra [11],[12] où la proie est le poisson et le prédateur la flotte de pêche. Ce modèle classique prévoit deux cas possibles :

• l’extinction de l’effort de pêche lorsque les coûts d’exploitation de la pêcherie sont élevés,
• sinon un équilibre stable de pêcherie durable.

Afin d’obtenir un équilibre de sur-pêche conduisant à l’extinction du stock de poissons, il est nécessaire de rajouter la troisième équation avec un prix variable. Le cas le plus simple de fonction demande est celui d’une droite de pente négative dont l’étude a été réalisée et prédit le cas de pêcheries en état de surexploitation avec des prix qui flambent pendant que les captures s’effondrent [16].

Le choix d’une fonction demande linéaire est discutable car il implique l’existence d’un prix maximum au-delà duquel aucune demande n’existe. Or pour certaines espèces rares, les prix peuvent augmenter jusqu’à atteindre des valeurs considérables. Par exemple certains thonidés devenus très rares ont été vendus aux enchères au Japon pour plus d’un million de dollars, mettant en évidence que, même pour un prix très élevé, il existait une demande résiduelle. Il est donc judicieux de considérer le cas plus général d’une fonction demande non linéaire positive pour tout prix même très élevé.

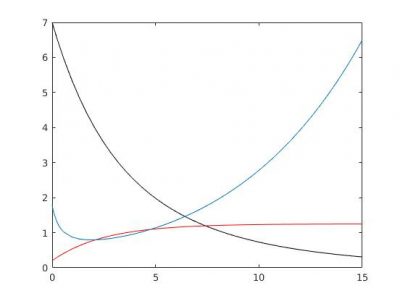
L’étude de ce type de modèle prédit des situations de surpêche avec l’extinction de la ressource tout en continuant à pêcher jusqu’au dernier poisson, avec un effort de pêche restant toujours élevé et un prix qui ne fait qu’augmenter (Figure 7).

Les données disponibles sont souvent partielles et incomplètes. Ces modèles mathématiques permettent avant tout de prédire l’évolution qualitative de la pêcherie, notamment les grandes tendances comme l’effondrement du stock ou son maintien, la variation de l’effort de pêche, ou encore la flambée ou la stabilisation du prix sur le marché.

La Figure 8 montre la variation du prix du thiof sur le marché au Sénégal avec une augmentation importante du prix des années 80 jusqu’en 2006 dans une période où les captures se sont effondrées. Le modèle précédent est donc en mesure « d’expliquer » les données concernant la pêcherie du thiof en prédisant l’extinction de l’espèce résultant d’une surpêche avec un prix qui ne fait qu’augmenter. D’autres auteurs avaient mentionné la possibilité de provoquer l’extinction d’espèces devenant rares et dont les prix sur le marché augmentent considérablement [17].

Des versions du modèle bioéconomique de pêche avec des termes non linéaires plus forts, notamment avec un terme de capture présentant un effet de saturation de la pêche pour une biomasse importante de poisson conduisent à des solutions périodiques comme des cycles limites ou encore des attracteurs plus complexes [18].

Dans la réalité, les pêcheries sont actives sur plusieurs sites de pêche qui sont régulièrement visités par les bateaux. Une technique de pêche consiste à placer des objets flottants en mer, lesquels exercent un pouvoir d’attraction important pour certaines espèces pélagiques [19]. Ces objets sont appelés des dispositifs à concentration de poissons (DCP, Figure 9). Les pêcheurs viennent les visiter régulièrement pour capturer les poissons qui s’y agrègent.

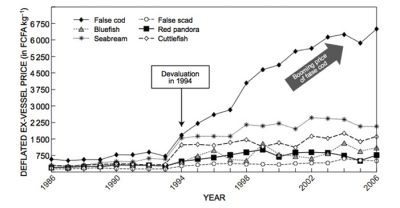
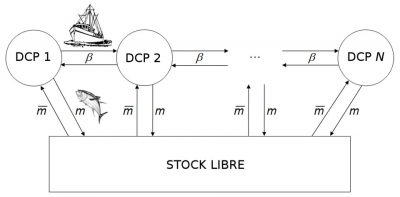
La plupart des modèles mathématiques récents prennent en compte la spatialisation des pêcheries pour permettre d’étudier le contrôle d’une pêcherie multi-sites (Figure 10) [20]. Est-il possible de quitter une situation de surpêche qui à terme provoquerait l’extinction de l’espèce surexploitée ? Une étude récente a ainsi montré qu’il est possible de sortir d’un état de surpêche pour aller vers un état de pêcherie durable sans risque d’extinction pour l’espèce exploitée, en faisant varier le nombre de sites de pêche et les coûts d’exploitation de la pêcherie [21]. Cette dernière étude pourrait expliquer le changement de tendance observé pour la pêcherie du thiof en Afrique occidentale où les débarquements ont commencé à augmenter à nouveau après une baisse importante, et les prix à baisser après une période de forte croissance. Le passage du cas de surpêche vers le cas d’une pêcherie durable pourrait donc résulter de la décision des pêcheurs sénégalais de partir pêcher le thiof sur des sites de pêche de plus en plus lointains, en Mauritanie, Gambie, Guinée et Sierra Leone, avec des coûts d’exploitation de plus en plus élevés.

De nombreux autres aspects peuvent être pris en compte dans les modèles bioéconomiques de pêcherie, notamment la structure des poissons en stade (œuf, larve, juvénile, adulte) ou encore les interactions avec les autres espèces de l’écosystème. Cependant, l’existence d’équilibre de surpêche conduisant à l’extinction de l’espèce commerciale et à l’arrêt de la pêche est un résultat qui reste robuste pour une large palette de modèles mathématiques et informatiques.

5. Messages à retenir

• Les interactions trophiques au sein des écosystèmes marins dépendent de la taille des individus.
• Une exploitation ciblant les espèces en fonction de leur taille aura des effets en cascade sur l’ensemble des niveaux trophiques d’un écosystème marin.
• Les extinctions globales d’espèces marines sont rares, mais leur extinction locale, ou la disparition de leur rôle écologique ou économique, sont fréquentes.
• Une grande partie des espèces de poissons commerciales sont surexploitées.
• Une gestion des ressources marines doit s’appuyer sur des outils d’aide à la décision permettant aux gestionnaires et aux décideurs de prendre des mesures de conservation et d’exploitation optimale des pêcheries.
• La modélisation mathématique permet de prévoir les effets des aménagements du littoral et des mesures de contrôle de la pêche.
• Une pêche par quota fixe est plus risquée qu’une pêche sans contraintes car elle peut provoquer l’extinction de l’espèce.
• Le couplage des dynamiques écologique et économique prédit des situations de surpêche provoquant l’extinction de la ressource avec un effort de pêche restant élevé et un prix ne faisant qu’augmenter.

 

---

Références et notes

Image de couverture. Banc de poissons. Source : Andrepiazza [CC BY-SA 3.0], via Wikimedia Commons.

[1] Cury, P., Miserey, Y., 2008. Une mer sans poissons. Calmann-Lévy.

[2] Cury, P., Shannon, L., Shin, Y.J., 2003. The functioning of marine ecosystems: a fisheries perspective, in: Sinclair, M., Valdimarsson, G. (Eds.), Responsible Fisheries in the Marine Ecosystem. CAB International, Wallingford, UK, pp. 103–123.

[3] Pauly, D., Christensen, V., Dalsgaard, J., Froese, R., Torres, F., 1998. Fishing down marine food webs. Science 279: 860–863.

[4] Jackson, J.B.C., Kirby, M.X., Berger, W.H., Bjorndal, K.A., Botsford, L.W., Bourque, B.J., Bradbury, R.H., Cooke, R., Erlandson, J., Estes, J.A., Hughes, T.P., Kidwell, S., Lange, C.B., Lenihan, H.S., Pandolfi, J.M., Peterson, C.H., Steneck, R.S., Tegner, M.J., Warner, R.R., 2001. Historical overfishing and the recent collapse of coastal ecosystems. Science 293: 629–638.

[5] Courchamp, F., Angulo, E., Rivalan, P., Hall, R.J., Signoret, L., Bull, L., Meinard, Y., 2006. Rarity Value and Species Extinction: The Anthropogenic Allee Effect. PLoS Biol 4, e415.

[6] Burgess, M.G., Costello, C., Fredston-Hermann, A., Pinsky, M.L., Gaines, S.D., Tilman, D., Polasky, S., 2017. Range contraction enables harvesting to extinction. PNAS 201607551.

[7] McCauley, D.J., Pinsky, M.L., Palumbi, S.R., Estes, J.A., Joyce, F.H., Warner, R.R., 2015. Marine defaunation: Animal loss in the global ocean. Science 347: 1255641.

[8] Degnbol, P., Gislason, H., Hanna, S., Jentoft, S., Raakjær Nielsen, J., Sverdrup-Jensen, S., Clyde Wilson, D., 2006. Painting the floor with a hammer: Technical fixes in fisheries management. Marine Policy 30: 534–543.

[9] Pikitch, E.K., Santora, C., Babcock, E.A., Bakun, A., Bonfil, R., Conover, D.O., Dayton, P., Doukakis, P., Fluharty, D., Heneman, B., Houde, E.D., Link, J., Livingston, P.A., Mangel, M., McAllister, M.K., Pope, J., Sainsbury, K.J., 2004. Ecosystem-based fishery management. Science 305: 346–347.

[10] Thiao, D., Chaboud, C., Samba, A., Laloé, F., Cury, P., 2012 Economic dimension of the collapse of the ‘false cod ‘ Epinephelus aeneus in a context of ineffective management of the small-scale fisheries in Senegal. Journal of Marine Science 34(3): 305–311.

[11] Auger, P., Lett, C., Poggiale, J.-C., 2015. Modélisation mathématique en écologie, cours et exercices corrigés. Dunod, Paris.

[12] Murray, J.D., 1989. Mathematical Biology, Springer-Verlag, Berlin Heidelberg.

[13] Clark, C, 1976. Mathematical bioeconomics: the optimal management of renewable resources, New York, Wiley-Interscience.

[14] Beddington, J.R., May, R.M., 1977. Harvesting naturel populations in a randomly fluctuating environment. Science 197: 463–465.

[15] Ly, S., Auger, P., Balde, M., 2014. A bioeconomic model of a multi-site fishery with non linear demand function: Number of sites optimizing the total capture. Acta Biotheoretica 62 (3): 371–384.

[16] Auger, P., Mchich, R., Raïssi, N., Kooi B., 2010. Effects of market price on the dynamics of a spatial fishery model: Over-exploited fishery/traditional fishery. Ecological Complexity 7: 13–20.

[17] Holden, M.H., McDonald-Madden, E., 2017. High prices for rare species can drive large populations extinct: The anthropogenic Allee effect revisited. Journal of Theoretical Biology 429: 170–180.

[18] Bergé, P., Pomeau, Y., Vidal, C., 2004. L’ordre dans le chaos, Hermann.

[19] Dagorn, L., Holland, K.N., and Itano, D.G. 2007. Behavior of yellowfin (Thunnus albacares) and bigeye (T. obesus) tuna in a network of fish aggregating devices (FADs). Mar. Biol. (Berl.), 151(2): 595–606.

[20] Auger, P., Lett, C., Moussaoui, A., Pioch, S., 2010. Optimal number of sites in artificial pelagic multisite fisheries. Canadian Journal of Fisheries and Aquatic Sciences 67(2): 296–303.

[21] Brochier, T., Bah, A., Thiao, D., Brehmer, P., Auger, P., Ly, S., Nguyen-Huu, T., 2018. Can overexploited fisheries recover by self-organization? Reallocation of fishing effort as an emergent governance. Marine Policy 95: 46–56.