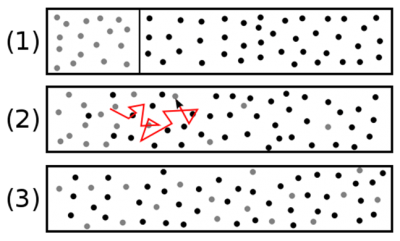
扩散,充分混合过程中极为关键的一步

空气中的二氧化碳(CO2)或咖啡中的糖等化学物质,即使处于静止状态,一段时间后也会与周围的流体完全混合。热量也会通过静止的物体在同样的传输机制下传递,直到温度变得均匀为止。类似地,在存在摩擦的流体层中,作用于流体表面上力会在流体层的整个厚度上传递。在流体环境中,湍流能促进其组分的分散,但是这种分散并没有达到分子的尺度。正是这种分子的无序运动才完成了这一我们称之为扩散的输运过程。我们还发现,分子扩散是一个非常缓慢的过程,但湍流能显著促进扩散。
“diffusion”一词的含义不尽相同,但所有解释的共同点是:某种量通过介质基本组成粒子的搅动而分散到周围介质中的输运过程。在物理学中,我们要区分下面两种类型的扩散现象:
- 一种是基于介质中原子或分子无序运动属性而产生的传输现象,其特征在于输运量的分布会趋于均匀。这个量可以是特定化学物质的浓度、热量或是动量。最终达到的均匀状态即为环境的热力学平衡状态。
- 另外一种是非均匀介质中波的衍射现象,这种波可以是像光之类的电磁波,也可以是声波。这些现象也会在本百科全书中的其他文章中介绍,如《天空的颜色》和《声音的发射、传播和感知》。在英语中,这种波的衍射现象也被称为“散射”(scattering),但我们应将其与扩散(diffusion)现象本身相区别。
在日常用语中,“diffusion”一词也有不同的含义,它既可以指对公众的知识的传播,也可以指通过无线电(无线电广播)或电视(电视广播)实现各种类型的信息传递。
1. 静止的空气:一群躁动不安的分子
文章《地球的大气层和气体层》中提到,干燥空气的主要成分有氮气(71%)、氧气(28%)、氩气(少于1%),还有其他含量更少的气体。气体分子会充满所有可用的空间,这是气体有别于其他凝聚态物质(液体或固体)的一种属性。固体或液体有特定的体积,固体还有自己固定的形状。
[来源:© 瑞内·莫罗(René Moreau)]
2. 气体的分子参数与宏观属性之间的关系
通过感知和测量,我们可以很容易地将分子世界的这些参数与一些宏观量相关联。《压强、温度和热量》一文对压力p,温度T,单位体积的质量(密度)ρ和粘度[3]μ这些物理量之间的关系已经做了分析,从中我们可以得到分子尺度与宏观尺度之间的第一个关系:m = M/NA,NA = 6.022×1023 mol-1,即每个分子的质量m等于摩尔质量M除以阿伏伽德罗常数(每摩尔中的分子数)。并且密度ρ等于单位体积中的分子数量n乘以每个分子的质量,这样我们就得到了两种尺度参数之间的第二个关系:ρ = nm。
为了将气态介质中某一点的压力p与气体分子的参数联系起来,我们假设在该气态介质中的某处有一个单位面积的固平面(S = 1,单位可任意选择)。单位时间内该平面的两侧会不断地受到气体分子从各个不同方向的撞击和动量积累,在这一过程中气体分子失去并重新获得动能,每个分子的动能为mc2/2。由此,施加在单位表面上的压力p平均为nmc2。考虑到气体分子的真实速度[4]和实际相撞速度,经严格的推算可得到压力的表达式为p = nmc2/3,其中系数1/3修正了由于我们简化模型估算而带来的误差。从而我们得到了气体分子参数(n,m,c)和宏观属性(压力p)之间的第三个关系。
由上面的几个关系式我们知道压力和密度都与分子的参量相关,可由理想气体状态方程表示出温度与压力的关系:p/ρ= RT/M,其中R = 8.314 m3 ·Pa·mol-1·K-1,R为理想气体常数,M为气体混合物的平均摩尔质量。这样我们就得到了第四个关系式[5]:T = Mc2/3R,这个表达式强调了温度T和分子的速度平方c2之间的正比例关系(详见文章《压强、温度和热量》)。
除此之外,还有一个表示气体动力学粘度的关系式:μ=nmcλ/3,这个关系式将会在本文第5节中说明。由此,海平面处的空气,通常具有以下值:
p = 1.013105 Pa ,T = 288 K , ρ = 1.22 kg·m-3 , ν = 10-5 m2·s-1 ,
由上述的五个关系式可以得到:
n = 2.51025 m-3 ,m = 4.810-26 kg ,c = 497 m·s-1 ,
d = 3.410-9 m ,σ = 0.4610-9 m ,λ = 610-8 m 。
为了对分子世界的尺度有一个更准确的认识,我们可以从上述计算结果中得知,边长为1微米的小立方体包含约2500万个气体分子,且两个相邻分子之间的距离(d)约为其直径(σ)的7倍,平均自由程(λ)约为60 nm,是分子直径的130倍,并且分子的平均速度(c = 497 m·s-1)比声速(340 m·s-1)略高。
3. 气体扩散机制
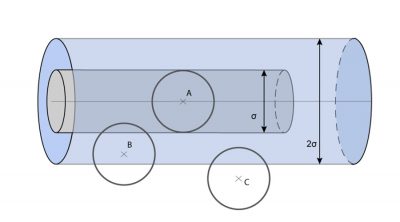
[来源:© 瑞内·莫罗(René Moreau)]
然而,建立这种平衡所需的时间比分子两次碰撞的间隔时间(λ/c ≈ 1.4×10-10s)长得多(几小时或更久)。因此在非平衡状态下气体分子的碰撞会非常频繁,如果碰撞后的分子都具有相同的G值,即G/n(G为单位体积的值),我们就说气体处于局部平衡的状态。
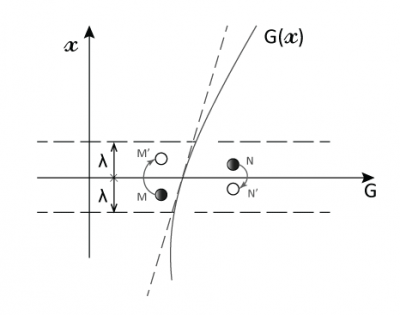
穿过平面x = 0(如图3)的分子的G值平均为G/n,其运动距离约等于平均自由程λ。因为与宏观尺寸相比λ极小,所以G(x)在x = 0附近可用其斜率为Γ0的切线替代,这样就可以得到一个简单的分布:G = G0 + Γ0x。我们进一步假设:对于来自x> 0侧的分子G+ = G0 + Γ0λ,对于来自x <0侧的分子G– = G0 – Γ0λ。
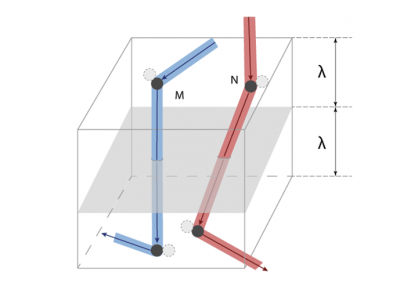
[来源:© 瑞内·莫罗(René Moreau)]
要估算G通过该单位面积截面的净流量,须将G的前后之差γ0λ乘以单位时间内穿过该截面的分子数。在该单位面积上方的体积中(如图5),有nλ个分子,每个分子在单位时间内发生c/λ次碰撞,所以在该体积内单位时间发生的碰撞次数约为nc。但是只有碰撞后朝向该截面的分子才会穿过该面,由此进一步计算得出单位时间内穿过该截面的分子数为nc/3(系数也是1/3)。
最后,可以通过关系式φ = (cλ/3)dG/dx来估计平面x = 0上单位面积的G的流量φ。由此我们可以得到如下结论:如果G的分布不均匀,则通过分子搅动传输的G的净流量与该区域G的局部梯度dG/dx成正比,可以用φ = -DdG/dx表示。通常,我们在式中加上负号“-”,这样当dG/dx为负时(比如热量从热侧流向冷侧),流量则为正。其中系数D = cλ/ 3,称为气体的扩散系数,它是纯粹的运动学参量,单位是m2/s。扩散系数反映了气体扩散能力的大小,与气体自身的性质无关。
用第2节中给出的数值可以估算出空气的扩散系数。当c = 497 m·s-1和λ = 6×10-8 m时,可得出D ≈ 10-5 m2·s-1。为了使该数值更具有实际意义,让我们回到图4所示的实验中:设容器的长度为L,因为扩散系数是长度的平方除以时间(L2T-1),所以达到最终平衡状态所需时间为L2/D。如果L ≈ 10cm,则扩散持续的时间约为一个小时。倘若要使这个过程的持续时间约为1秒,则图4中的容器长约为1毫米,与小气泡相仿。
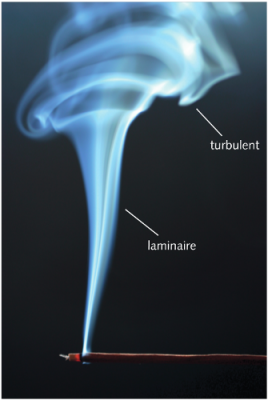
4. 湍流扩散
我们在生活中遇到的大多数流体中,如空气和水,湍流几乎是无处不在的。这是一种与分子运动完全无关的紊乱现象。在诸如风或洋流之类的流动中,湍流大范围存在,有显著的、可测量到的速度脉动。即使没有强加的流动,仅由于流体的动力学不稳定性[6],湍流也会以一系列大小不一的涡的形式存在。这与前面几节所谈到的分子搅动有相似之处,然而,宏观涡的大小要远大于分子的平均自由程,于是普朗特(Prandtl)[7]定义了一个新的量:混合长度[8],类似于气体分子的平均自由程。
[来源:© 克鲁诺斯拉夫·克内泽维奇(Krunoslav Knezevic)]
混合长度的概念非常模糊,但它的数量级却可以有很高的精确性,特别是存在边界层的情况下(如图7所示)。普朗特(Prandtl)提出在边界层内混合长度的表达式为l = κy,其中y是到边界的距离,κ是根据不同条件确定的常数。有了混合长度l的表达式,就可以用u’ ≈ l dU/dy估算距边界为y处速度脉动的量级。类比气体扩散,引入了类似分子扩散系数(D =cλ/3)的概念,用u’代替c、用l = κy代替λ,则边界层内的湍流扩散系数Dt为:Dt ≈ u’l ≈ κ2y2 dU/dy。
举例来说,在我们所处的厚度约为几百米的大气边界层内,距地面y ≈ 10 m处,假设空气的平均速度约为10 m·s-1,dU/dy ≈1 s-1,由实验得到的常数κ的值为0.1,则可计算出湍流的扩散系数Dt ≈ 10 m2·s-1,它是分子扩散系数的一百万倍。所以获得湍流混合物所需的时间约为十分之一秒:t ≈ l2/Dt ≈ 0.1s。但是这种混合是不完全的,因为各成分仅能扩散到最小的涡的尺度,这个尺度取决于流体的粘度。在大气中,边界层的厚度约为1毫米。我们知道分子搅动达到分子尺度的混合所需要的时间为L2/D。在现实中,分子扩散达到毫米尺度时就开始于与湍流的涡的扩散并存了。由此我们可以进行简化,假设分子扩散仅在毫米量级以下起作用。当L ≈ 10-3m,D ≈ 10-5m2· s-1时,我们得到扩散的时间尺度仍为十分之一秒左右。
从这些估算中我们可以得到如下结论:
- 湍流扩散只能到达最小的涡的尺度。
- 分子扩散将继续完成混合过程,两种机制的时间尺度均在十分之一秒。
- 如果不存在湍流,完全混合所需的时间将达到数小时。
5. 质量扩散和热扩散
通常用质量扩散率来表示化学物质在其所处流体中的扩散。假设流体(气体或液体)中的某些分子与其它分子不同,例如气态的水分子(H2O),处于较大的液体区域(例如宁静的湖泊)上的静止空气中。记C为在任一高度z下空气中水的体积浓度。参照上面推导出的公式,水蒸气向高海拔处扩散的净流量的表达式为φ = –DdC/dz,这就是菲克定律。要计算出水从低海拔处质量扩散的量,还要补充质量平衡以及初始条件和边界条件。
热扩散率的表达式是由通过分子搅动进行热传递的过程推导得来。假设G是气体单位体积的内能E,则有dE = ρCvdT,其中dT表示无穷小的温度变化量,Cv为气体的定容热容。所以内能,即热量的扩散传输可表示为φ = –ρCvDdT/dz。通常将该等式的以下两种形式都称为傅立叶定律:φ = –kdT/dz(其中k = ρCvD = Cvnmcλ/3为气体的热导率);或φ = –αρCpdT/dz(其中α = k/ρCp为气体的热扩散率,Cp是气体的定压热容)。
上述气体,特别是空气的物理性质(D,k,α,μ,ν)与分子参数n,m,c和λ有关。其中,对于给定密度的气体,只有分子的速度c可能随温度T变化,可以表示为:T = Mc2/3R = mc2/3kB。由此可以推断出气体的扩散系数(D,k,α,μ,ν)随着其温度的平方根一同变化。
6. 动量扩散:粘度
假设上述概念对沿着壁面流动的宏观流体仍然适用。只要这个宏观流动的时间(通常为数秒或数分钟)远大于分子两次碰撞间隔的时间(约10-11 s),就可以证明这个假设是正确的。

当z = 0不是壁面与流体的界面,而是两个流层之间的界面时,上面的结论也同样适用。当两个流层之间的界面以速度u流动时,牛顿粘性定律也可以表示流层之间相互作用的切向力,通常称之为摩擦力。这个沿速度方向的切向力会与和界面垂直方向的压力叠加(详见《压强、温度和热量》)。
7. 液体中的扩散机制
实际上所有液体都有自己的体积,这说明组成它们的分子彼此靠得很近。相邻分子之间的平均距离取决于施加在该液体上的压力,分子间距在通常情况下(p ≈ 103hPa)比分子尺寸稍大,为10-10~10-9m。这些分子的热运动,或称分子振动,使液体介质具有了一定的扩散能力,但是其扩散能力远弱于气体。这主要是因为液体中分子的作用半径小于其自身大小,而在气体中分子的作用半径即平均自由程,约为分子大小的25倍。这就解释了为什么在咖啡里加糖后需要用勺子搅拌。
存在于液体介质中的任何与介质分子不同的粒子都会不断地受到整体振动的影响,与气体介质中类似,这些粒子会从多的一侧流向少的一侧。该通量仍可以用菲克定律来表示:φ = -DdC/dx,其中D表示液体中粒子的扩散系数,C为其体积浓度。
为了了解液体的质量扩散率,从而反映其传输另一种物质的能力,爱因斯坦在1905年提出了如下定律[11]:D = kBT /6πμr,其中kB = 1.38×10-23J·K-1是玻尔兹曼常数,T是绝对温度,μ是液体的动力粘度,r是被输运粒子的半径。在一个r ≈10-9m、μ ≈10-3Pa·s的液体环境中,例如水,当环境温度为300 K时,我们得到D ≈ 2×10-10m2·s-1,比气体的扩散率小了约10000倍。爱因斯坦的公式中含有温度T,这表明分子热运动是扩散背后的真正驱动力。而分母中包含μ和r则意味着粘度与扩散率呈反比例关系,粒子的半径越大,扩散就越困难。
对于水和所有电绝缘液体而言,它们的热扩散率和质量扩散率差不多。但是对于液态金属来说,电子的热传导也是一种主要的传热机制,比质量扩散要重要得多。最著名的例子是液态钠用于冷却超再生器型核反应堆,如“凤凰号”,这一反应堆位于马尔库尔(Marcoule),1973年至2010年期间一直在运行。在300 K左右的温度下,液态钠的热扩散系数约为7×10-5 m2·s-1,比它的质量扩散率要高出10000倍。
8. 总结
- 混合物中特定参量或物质的扩散,如热量和动量,是由其基本粒子即分子或原子的搅动引起的。这是一种非常缓慢的输运机制,但却是微观尺度上的主导机制。
- 在空气和水等粘度不太高的流体中,湍流会促进质量、热量或动量的分散。但是这种机制下的最小尺度不能小于由粘度控制的最小的涡的尺度(通常大于一微米),小于这个尺度的扩散过程则由分子扩散继续作用来完成混合。
- 扩散定律起初是凭经验发现的,然后才发展成为理论模型。在稀薄气体(例如空气)中相对来说比较简单,本文已进行了概述。而在液体环境中则复杂得多,目前仍在研究中。
参考资料及说明
封面图片:在日出之前乡村宁静止的空气中,植被呼吸作用释放的物质通过扩散作用传输到空气中。
[1] 纳米是米的十亿分之一(10-9m),微米是米的百万分之一(1μm= 10-6m)
[2] 路德维希·玻尔兹曼(Ludwig Boltzmann,1844-1906),奥地利物理学家、哲学家,提出了一种名为“硬球”的分子模型,由该模型推导出了一个以他名字命名的方程。
[3] 通常用运动粘度ν代替,运动粘度ν是动力粘度μ与密度ρ之比,即ν=μ/ρ。
[4] 所有这些速度矢量,包括其各自的方向和值,都可用麦克斯韦分布函数表示。但计算较复杂,超出了本文涉及的范围。
[5] 通过引入与R相关的玻尔兹曼常数kB和阿伏伽德罗常数NA = 6.0248×1023,kB= R/NA = 1.380×10-23 J/ K,该表达式可更好地表示为kBT = mc2/3(焦耳热用开氏温度表示)。
[6] 例如在黎明时太阳升起,地表开始变暖,地面就会通过热扩散加热最低层的空气,使低层的空气比上方的空气更轻。这种较重流体位于较轻流体上方的情况是不稳定的。
[7] 路德维希·普朗特(Ludwig Prandtl,1875-1953),德国物理学家,慕尼黑大学教授,对流体力学做出了重要贡献。他以边界层理论、混合长度的概念和有限翼展机翼升力计算的简单理论而著称。
[8] Lesieur, 湍流(Turbulence), 法国EDP Sciences出版社, 格勒诺布尔科技出版社(Grenoble sciences collection), 2013, p. 128.
[9] 通过建立位于壁面z> 0侧的小的气域的整体平衡,得出φ = –τ,该小气域对流体施加-τ的切向力,这种整体平衡的表述通常称之为动量定理。
[10] 这种表述是由纳维叶(Navier)和傅里叶(Fourier)等人建立的(详见《扩散之父》(《Fathers of the diffusion concept》))。
[11] 阿尔伯特·爱因斯坦(Albert Einstein),布朗运动理论的研究(Investigations on the Theory of the Brownian Movement),多佛出版社(Dover Publications),Inc. (1985), (ISBN 0-486-60304-0). 重新发行了爱因斯坦关于布朗运动理论的原文。
环境百科全书由环境和能源百科全书协会出版 (www.a3e.fr),该协会与格勒诺布尔阿尔卑斯大学和格勒诺布尔INP有合同关系,并由法国科学院赞助。
引用这篇文章: MOREAU René (2024年4月12日), 扩散,充分混合过程中极为关键的一步, 环境百科全书,咨询于 2025年4月15日 [在线ISSN 2555-0950]网址: https://www.encyclopedie-environnement.org/zh/physique-zh/diffusion-ultimate-step-good-mixture/.
环境百科全书中的文章是根据知识共享BY-NC-SA许可条款提供的,该许可授权复制的条件是:引用来源,不作商业使用,共享相同的初始条件,并且在每次重复使用或分发时复制知识共享BY-NC-SA许可声明。