运动物体受到的阻力

为什么人在水中移动如此困难?为什么大型船只需要消耗那么多的能量来克服水的阻力?而在如此轻盈的空气中,鸟类、骑自行车的人、汽车和飞机又是如何克服这份阻力前进的呢?也正是这种因空气的黏粘性而产生的阻力(黏粘性阻力),阻止了雾滴和其他微小颗粒的下落。对于车辆或其他大型物体,它们的阻力还来源于湍流(紊乱的流动)阻力,它与流体位移造成的能量损失有关。而水面上的船只会通过另一种机制损失能量,这一机制与重力有关——船体与水的相互作用使得船的周围产生波浪,从而产生了兴波阻力。
1. 黏粘性阻力:以雾和雨为例
1.1. 黏粘性摩擦

想象一个薄如刀片的平板在蜂蜜或油这样黏粘稠的液体(图1)中运动,即使是低速运动,平板也必须克服流体摩擦产生的阻力才能向前运动。从局部看,该板的每个表面单元都受到与运动方向相反的切向力。切向力的大小与流体的黏粘度(见文章《流体和固体》)以及壁面附着流体的法向速度梯度成正比。
从整体看,这些由局部力构成的阻力产生的结果就是黏粘性摩擦效应。掉进蜂蜜里的勺子下落和流线型锥形船体缓慢运动都属于这种情况。物体周围的流动称为层流,这意味着每个流体颗粒的运动都比较规则,相邻的流线也比较规则。这种行为与下面讨论的湍流状态不同。
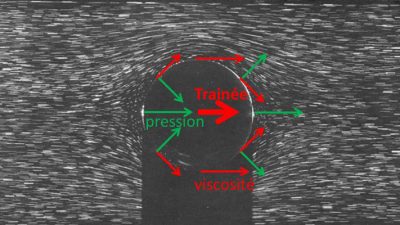
小球在流体中的缓慢运动(图2)是一个非常著名的实验,因为球体的几何形状简单,并且小水滴或气泡受表面张力作用也会形成类似形状。通常,我们并非在静止的流体中观察物体的运动,而是在与球体固结的参考系中观察流动。
小球所受的黏粘性阻力可由斯托克斯公式[1]得到,根据该公式,阻力F大小与球体的直径d及其相对于周围流体的速度U成正比,即F=3πµdU。该定律在考虑动力黏粘度μ的情况下可适用于蜂蜜、水、空气或任何其它普通流体(统称为牛顿流体)。实际上此类公式适用于缓慢运动的任何小物体,3π特指球形物体阻力公式的系数。和摩擦力一样,阻力总是与速度方向相反,大小成正比。
1.2. 小物体自由落体的速度限制
在真空中,受重力的作用,任何物体——无论是铅块还是羽毛,都会以同样的加速度匀加速落下(见《动力学定律》。在水或空气等流体中,物体也要受到阿基米德浮力,这正是静水压力的结果(见《阿基米德的浮力和升力》。这种力与被物体所排挤出流体的重力大小相等,方向相反,因此,物体将以较小的加速度下降或上升——这取决于它与周围流体密度的相对大小。
但物体不会无限加速下落,因为阻力随着速度的增加而增加,直到完全平衡了由它的重力和阿基米德浮力产生的驱动力。这时,物体所受的合力为零,根据动力学定律,它的加速度就为零。此时速度所达到的恒定值被称为下降速度极限。对于我们这里考虑的轻小物体来说,很快就能达到这个速度极限。请注意,比周围流体轻的物体,如水中的一个气泡或一滴油,会向上运动。
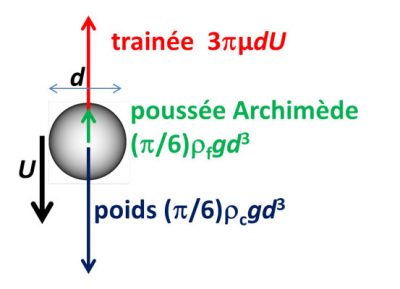
利用上面给出的斯托克斯公式,可以很容易计算出来最大下降速度。重力是重力加速度g≃9.81m·s–²乘以球体的体积 (1/6)pd³,再乘以球体的密度ρc。阿基米德的浮力由同样的公式给出,用流体的密度ρf代替物体密度ρc。通过三个力的平衡(见图3),我们可以推导出最大下落速度等于 (1/18)g(ρc-ρf)d²/µ。最大下落速度不仅随着粘度μ增大而降低,而且随着直径d平方的增大而增大,这就是为什么小物体能长时间保持悬浮状态的原因(见焦点:《小物体悬浮的世界》)。
1.3. 雾随风动
假设一个直径约为20微米(0.02毫米)的雾滴,考虑到水的密度(1000 kg·m-3)和空气的黏粘度(μ= 2*10-5 kg·s-1·m-1),该液滴的最大下降速度约为1 cm·s-1。然而,周围空气的轻微运动都比这个速度大得多。在这种条件下,液滴保持悬浮状态,随风而动。这同样适用于花粉和所有直径小于20微米的颗粒。这也就解释了为什么在美丽的高空中,大气平静时污染峰值持续时间很长。
因此,当雾产生时,导致雾消失的机理并不是雾落到地面上,而是雾在阳光照射后蒸发,或者是随着温度降低,在寒冷的地面上以露水或霜的形式凝结。
1.4. 从雾到雨
在充满水汽的云中,水滴会凝聚产生越来越大的水滴。当其直径达到约一毫米时,就会像雨一样落下来。如果气流仍然是层流,此时直径d=2毫米的水滴,比细小的雾滴大100倍,其下降速度将是雾滴的10000倍,可以达到100m/s(360km/h)。实际上,此时空气阻力为湍流情况的阻力,摩擦力增加,自由落体速度降低(我们后面也会讲到)。
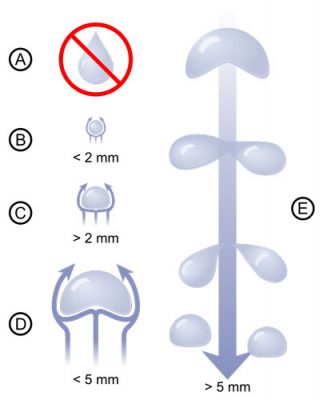
此外,在毫米尺度上,表面张力已经不足以维持液滴的球形。如图4所示,液滴在空气流动引起的压差阻力作用下发生变形。如果液滴的尺寸超过5mm(见图4. E),就会变得不稳定,从而发生液滴的破碎,重新形成2mm左右的液滴,因此液滴下落的整个过程就是B、C、D、E的不断循环的过程。
2. 湍流阻力
2.1. 雷诺数
当一个足够大的物体在空气或水这样低黏粘度的流体中运动时,流动就会变得不稳定。这种不稳定性也是落叶不规则运动的根源。在较高的速度下,就像船只驶过后留下的湍流尾迹那样,在物体的下游会形成一个无序涡流尾迹(见焦点《湍流尾迹》)。
爱尔兰物理学家和工程师奥斯本·雷诺(Osborne Reynolds)首次对湍流概念进行了科学定性[2]。为了纪念他,流体力学中最重要的无量纲量用他的名字命名,称为雷诺数。这个数,记为Re,等于流动的黏粘性扩散时间尺度(可估计为d²/ν,其中ν为运动黏粘度[3])与流体绕过障碍物的时间尺度(约为d/U)之比。所以,雷诺数的表达式为Re=Ud/ν。当雷诺数超过一个临界值时,就会发生湍流,这个临界值总是比1大得多,具体取决于所考虑的流动情况。
尽管湍流这一现象非常复杂,且建模仍然是个问题,但雷诺数体现了流体(甚至不同黏粘度的流体)围绕几何形状相同但大小不同的物体流动的相似性规则。例如,我们可以预测,在相同的流体中,如果一个物体尺度扩大了10倍,那么它的速度需要减小到原来的1/10才能形成相似的湍流流动。在实践中,如气球、汽车或船等这些相当大的物体的尾部总是存在湍流。
2.2. 阻力系数
通过这种雷诺相似性可以得到湍流阻力的表达式为F=(1/2)Cx S ρf U2,其中Cx称为阻力系数。该力大小与物体的最大迎风面积S(也称为主迎风面积[4])成正比,同时也与前面提到的流体密度ρf和相对运动速度的平方U²成正比,阻力系数Cx取决于物体的形状,也取决于雷诺数。

对于一个处于层流中的球体,通过上面提出的斯托克斯公式可以得到Cx=24/Re。另一方面,当雷诺数足够大时,Cx则会趋于定值,而这个定值只取决于物体的形状,这使得物体外形对减阻具有重要意义。图5显示了圆盘和球体的Cx与Re之间函数关系。Re在100到1000之间为层流到湍流的转捩区,当Re变得非常大时即湍流时,Cx趋于一个常数,但圆盘和球体的Cx最终趋于的常数不同。由于球体的外形优于圆盘,所以其Cx值较低。
要理解以上现象,可以估算物体在运动过程中排开流体所消耗的能量[5]。像圆盘这样整个截面的横扫运动对应的阻力系数Cx≃1,而流线型的物体推开流体的所需的力就小得多,它减少了湍流尾迹的横截面大小。减阻性能最好的汽车阻力系数可以达到Cx≃0.25。事实上,控制阻力的是CxS乘积,可以看作是有效面积,用它和流体密度、速度的平方的乘积就很容易计算出阻力了。
2.3. 消耗功率与速度的立方成正比
阻力造成了能量损失,即阻力做了负功。相应的功率,或单位时间内的能量损失,是将阻力乘以运动速度得到的。由于阻力与U²成正比,消耗的功率就与U³成正比。因此,消耗功率随速度增加而急剧增长。
这种消耗的能量会转化为流体的动能(包含所有湍流脉动的动能),并在流体黏粘性的作用下最终耗散为热量。由于热量被稀释在大量的流体中,因此产生的温升一般难以察觉。但是,对于以极高速度进入大气层的陨石或航天器来说,产生的热量会使它们表面的温度上升到数千度并导致其毁灭。
2.4. 动压的作用:阻力和升力
物体缓慢运动所受的阻力是由黏粘度控制的,而快速运动的物体所受的阻力主要是由流动引起的压力差,称为动压。正如我们所看到的,这种压差阻力使其周围的流体在侧向绕开物体时从上游向下游流动,以至于运动的物体可以替换原来流体所在的位置。这种压力差会对运动物体整体产生阻力,从而阻碍物体运动。
物体在高速运动时,黏粘性效应可以忽略,利用伯努利方程[6]可以估算出流体的动压ρfU²。将这个动压乘以横截面积S,就可以得到上面所说的湍流阻力。实际上,控制阻力的是湍流尾迹的横截面积,大小为CxS,而不是物体本身的面积S。
对于不对称的物体,如飞机的机翼或风帆,通过表面压力积分还会得到与速度垂直的力,称为升力(见《阿基米德的浮力和升力》)。它和阻力都是力的分解,而阻力的方向与速度方向平行且相反。这两个力的大小均与流体的密度和速度的平方成正比,因此它们的比值是不变的。后面我们会知道,这个比值可反映飞机滑行能力,叫做升阻比。
2.5. 关于自由落体速度极值的例子
对于雾和雨来说,只要知道空气的运动黏粘度ν=1.5*10-5 m2/s,就很容易估算出雷诺数。对于雾滴,d = 20×10-6 m (或0.02 mm),U =10-2 m/s,雷诺数Re≃10-2,流动处于层流状态。而对于雨滴,直径d=2 mm,以速度为U=100 m/s下降的物体,雷诺数为Re=13000,处于湍流状态。但是,由于没有考虑湍流摩擦阻力,下落速度被高估了。若液滴的重量为(1/6)πgρfd3=4*10-5 N,用阻力系数Cx=0.5计算的湍流阻力进行平衡,下落速度达到6 m/s,对应的雷诺数Re≃800,刚好在湍流区的边缘。
假如一个人从高处自由下落,其质量M=80 kg,即重量为800 N,阻力可以用有效截面积CxS=1m2来估计,得出最快下落速度为50m/s,即180km/h。达到这一极限速度大约需要5s,落体高度为 (1/2)gt2 ≃125 m。因此,很快就会达到速度极限,随后,跳伞者在空中下落时,不再感觉到任何加速度。一旦降落伞展开,其横截面积CxS增加了100倍,意味着阻力增大100倍,速度极值就会大大降低。因此,要获得同样大小的阻力,速度就要下降到(因为与U²成正比),即5m/s。
2.6. 流体密度的重要性
如前文所述,湍流阻力大小与流体的密度成正比。在34000米的高度,空气的密度比地面附近低100倍,需要10倍的速度才能产生相同的阻力。因此,阻力与重力平衡时的最快下降速度值就要增大10倍,即500 m/s。2012年,跳伞运动员费利克斯·鲍姆加特纳(Felix Baumgartner)从39000米高空自由下跳,45秒后,在约30000米的高度,他的下落速度达到了372m/s(1340km/h),接近预估速度[7]。
在水里,阻力则要大得多,水的密度是低空时空气密度的800倍,这也解释了为什么固体在水中下落的速度要比在空气中慢得多(阿基米德浮力也会减慢下落的速度,甚至可以抵消重力,让物体漂浮起来。但对于石头等密度大的物体来说,它的作用要比阻力小很多)。
这种密度效应也解释了为什么一个人骑自行车速度可以达到40km/h,而优秀的游泳运动员游泳时的速度很少超过4km/h。速度增加10倍,则消耗功率增加1000倍(如前文所述,消耗功率与U3成正比)。但由于空气和水的密度不同,所以骑自行车的人和游泳运动员所消耗的功率大致相同。
3. 水面上的重力阻力(兴波阻力)

另一个减缓船舶行进的力是兴波阻力(wave drag),或叫重力阻力(gravity drag)。船艏的压力具有双重作用,正如我们所看到的,行进中的船艏把上游的水推向两侧,然后占据原来水的位置。但是拨开的水高度被提升,高于原来的水平面,随后向船的两侧回落。水在上升过程中获得的势能(图6)在其下降过程中转化为动能,下降到水平面以下。然后,水体上下振荡,像钟摆一样,形成远离船体的波动,这就产生了在船舷上看到的波浪。天鹅在平静的湖面上缓慢移动也会产生类似的波浪(图7)。这种重力阻力将船舶消耗的部分能量转移到波浪上,该阻力受重力影响。

我们已经知道,黏粘性和湍流尾迹取决于雷诺数(图5)。重力阻力由另一个参数控制,称为弗劳德数(Froude number)[8],它表示为Fr = U /(gl)1/2,其中l是运动物体的长度。经验表明,当弗劳德数接近1时,重力阻力会大大增加。此时所产生波的波长(两个连续的波峰之间的距离)就接近于船的长度[9]。船体将消耗相当大的能量来驾驭自己产生的波浪,而不是简单地提升附近水面。

图8与图7的情况明显不同。对于经典的船型来说,超过Fr=1这个极限几乎不可能。船必须更长才能更快。只有通过产生额外的升力,比如使用合适的船体(如帆板)或侧翼(水翼),船只才能超过这个极限(见《阿基米德的浮力和升力》。
4. 如何对抗阻力
尽管阻力再小,仍会降低运动速度。因此,只有在有驱动力与之平衡时才能维持运动状态不变。只要驱动力和阻力之差不为零,物体就会加速或减速,这取决于差值是正还是负。因此,在上面讨论的自由落体情况中,重力使物体加速,直到阻力准确地平衡了重力。
在没有动力的情况下,任何水平运动都会因阻力而减慢。因此,球和气球的水平速度沿其轨迹下降。速度的最大值来自最初的冲击力(网球或足球约为260km/h),而轨迹的长度则取决于阻力。例如,对于高尔夫球,世界冠军杰森·祖巴克(Jason Zuback)创下的速度记录是320km/h,轨迹总长度是400m。在竖直上抛运动中,不受阻力的情况下,物体达到的高度大概是受阻力情况的两倍。
4.1. 速度的能源成本
即使在没有逆风的水平道路上,骑车人也必须踩踏板来克服前进的阻力。其尾迹的横截面积CxS在0.2~0.4 m2之间,取决于其在自行车上的姿势,也就是迎风面积的大小[10]。因此,对于15m/s(54km/h)的骑行速度,阻力将在27到54N之间,骑车人为克服阻力输出的功率(由该力乘以速度求得)大约是400到800W,此外,还必须增加用于抵抗机械摩擦的功率,而机械摩擦几乎与速度无关。只有杰出的冠军才能持续几分钟输出400 W的功率[11](相比之下,一匹马所提供的平均功率——即常说的马力——约为735 W)。这就解释了为什么自行车选手一小时的骑行纪录恰好是54km(2015年布拉德利·威金斯(Bradley Wiggins)创下的记录)。如果将速度限制在12m/s(43km/h)则只需要输出近一半的功率,这会更容易实现。
一款外形优良的量产汽车,其CxS约为0.6m2。在速度为28 m/s (100 km/h)时,会产生280 N的阻力,或者说为了克服空气阻力需要输出8 kW功率。这对于一辆额定功率为50kW的普通汽车来说仍然是适度的。当速度达到200 km/h时,所产生的阻力也会增加到原来的4倍。因此,给定路程所要消耗的能量(等于力和位移的乘积)增大到原来的4倍。由于此时速度是原来的2倍,因此所需的功率(即单位时间内所消耗的能量)是原来的8倍,即需要64千瓦而不是8千瓦才能平衡空气阻力。这只有大马力汽车才能做得到。
4.2. 不同的推进模式
封面图中的划船者用桨向后划水时,可在水面上见到一个个清晰的旋涡。在这里,作用在桨上的是一种阻力,它推动着船前进。脚踏船和老式轮船也是同样的原理。
为飞机提供推进力的是螺旋桨或发动机。每个螺旋桨叶片的外形像飞机机翼,因此受到垂直于其转动平面的“升力”。在设计中需要加入扭矩,才能有效地产生向前的推力。在发动机的整流罩中,安装有大量桨片以优化运行。
鸟类扑翼飞行时,肌肉做功带动翅膀的扇动,每次扇动都会释放出旋涡(见《阿基米德的浮力和升力》),从而产生了升力和推力。游泳者的拍打(不管有没有游泳鳍)也会在其尾迹中释放涡流;它们的推进力正是来自这种机制。这也是一种垂直于鳍或翼挥拍运动的升力型推进模式。
4.3. 滑翔飞行

滑翔机的例子更加经典,经验丰富的飞行员会寻找上升气流,如热风,来引导飞机在空中上升。这时,风的阻力有一个向上的分量,增加了抬升作用,从而助力滑翔机上升。滑翔的鸟类,如海鸟和猛禽(图9),就广泛使用这些方法以减少它们的飞行能耗。
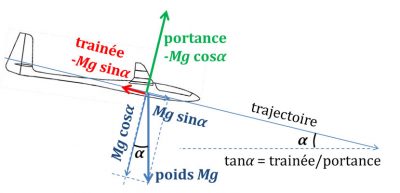
我们已经知道,升力和阻力与速度的平方成正比,它们的比值称为升阻比,也代表静止空气中物体下降斜率的倒数,如图10所示。那么,滑翔机在倾斜的平面上下降时,推动滑翔机的是重力Mg沿轨迹投影的分量,而其横向分量则由升力来平衡。效率最高的滑翔鸟——信天翁的滑翔比(升阻比)为20,与空客A320等客机相当(后者的滑翔比为17)。现代滑翔机做得更好,其升阻比约为50。在静止空气中,这样的滑翔机仅需要下降2000米,水平距离上就可以滑行100公里。
因此,飞行物体的速度受到如下约束:升力必须平衡重力,调整范围取决于其相对于轨迹的倾斜角。一架轻而大的滑翔机可以缓慢飞行,并利用上升的气流而上升。另一方面,为了飞得更快,飞机必须设计更小的翼展,代价是能量消耗更高。另一种策略是飞得更高:在1万米的高空,空气的密度比地面上低3倍,由于阻力和升力与速度的平方成正比,为了获得同样大小的力,速度需要增大到原来的3≃1.73倍。
5. 提高效率
5.1. 灵感来自于动物
观察动物世界,我们会发现很多例子,在飞行和游泳时最大限度减少运动的阻力。一些海豚能够在水中保持30km/h的游速,我们一直在寻找这种保持高速的神秘机制,比如它们通过皮肤弹性来抑制湍流等。但最近的研究表明,本质上,赋予它们惊人运动能力的是优良的身体外形和特殊的肌肉力量[12]。
至于鸟类,它们知道如何通过将腿缩进羽毛中,并尽可能贴合自己的轨迹方向来减少阻力。鱼鹰美妙的滑翔飞行(图9)很好地诠释了鸟类是如何进化身体结构,提高飞行技能以减少它们的飞行能耗的。
5.2. 控制湍流

在从自然界获得灵感的同时,科学和技术的进步也在为我们助力。汽车和飞机制造商使用了大量研究手段来最大限度降低阻力,从而减少燃料消耗,包括高性能数值模拟和风洞实验。使用烟雾令流动可视化(如图11),可帮助优化车辆的空气动力学外形,并测试每个细节的影响。
湍流是控制阻力的一个重要因素,人们对其展开了深入研究,以降低其影响,例如可以通过主动方法,或增加粗糙度或划痕等被动方法避免湍流扰动的增长,从而实现减阻。然而,这些方法存在着可行性和经济上的限制。以飞机为例,已知的限制阻力的解决方案是依靠机翼后半段的多个小孔吸收气流,从而使绕机翼的气流贴体,然而,由于小孔会堵塞,这并没有实施下去。在液体中,通过添加聚合物,即使是微量浓度的聚合物,也可以显著降低湍流阻力。当然,这只限于封闭环境下的工业应用,例如管道。
在赛艇中,人们使用翼型产生升力来减小兴波阻力取得了巨大进步。但要应用于运输船则会有许多问题。追求速度总是意味着巨大的能源消耗,这是提高效率所难以弥补的。
参考资料及说明
封面图片:桨手必须做功来克服独木舟的阻力,最终力的平衡决定了独木舟的速度。
[1] 斯托克斯(George Gabriel Stokes,1819-1903), 爱尔兰物理学家,在流动粘性效应的数学表达上做出了卓越贡献。
[2] 雷诺(Osborne Reynolds,1842-1912),爱尔兰工程师、物理学家,在流体力学中贡献卓越,特别是关于流动稳定性的开创性实验(1883),至今仍被引述。
[3] 流体的动力粘度,通常用μ表示,与流动的粘性摩擦力大小有关。单位是kg/(m∙s),有时叫做泊肃叶(poiseuille),以纪念19世纪法过物理学家泊肃叶(Jean-Louis Mare Poiseuille)。在研究中,流动的粘性也可用运动学粘度来表示,ν=µ/ρf,即流体的动态粘度与密度之比(参见文章Diffusion and propagation in air at rest),单位是m2/s。
[4] 严格地说,“迎风面”一词应指船体的竖直截面,“主迎风面”是最大的截面。因此这个海洋专业词汇被我们用来表示物体或航行器在流体中运动的等价面积。
[5] 在一个时间步长dt内,截面积为S的物体扫过的长度为Udt,则对应的流体质量为ρf SUdt。估算的动能为½ρfSU3dt,与阻力做功大小FUdt相当,这就得到阻力系数Cx=1。
[6] 伯努利(Daniel Bernoulli, 1700-1782),瑞士医生、物理学家、数学家、哲学家,巴塞尔大学的教授,他的主要兴趣是对流动的研究。伯努利定理,于1738年在出版的水动力学著作中发表,是流体力学的基础理论之一。它表述为沿着流线p+ρfU2/2=p0,其中p是当地压强,p0是来流制止的压强。
[7] 超过声速时存在额外的阻力:下落的能量不仅用于推开周围的空气,还使得空气压缩,形成激波,即一种高振幅声波,产生声障。船舶的兴波阻力则与此不同,它是与重力有关的。
[8] 这个无量纲数称为弗劳德数,弗劳德(William Froude, 1810-1879),英国工程师、海军建筑师,他是第一位研究重力阻力(兴波阻力)的科学家。
[9] 弗劳德数表达了船体速度与重力波传播速度之比,与波长l有关。尾迹波传播速度与船体的速度相当。速度关系即c≃U可用来估算尾迹波长,当Fr=1时,它与船体长度相当。
[10] 参考 http://sportech.online.fr/sptc_idx.php?pge=spfr_xfd.html
[11] 相对于总能耗,机械能的消耗大约为1.9kW,效率约21%,参考http://www.agoravox.fr/culture-loisirs/sports/article/puissance-et-performance-en-159520,这部分能耗与呼吸的氧吸收有关。
[12] F.E. Fisch and G.V. Lauder, 2006, Ann. Rev. Fluid Mech. https://www.yumpu.com/en/document/view/46389631/passive-and-active-flow-control-by-swimming-fishes-and-mammals.
环境百科全书由环境和能源百科全书协会出版 (www.a3e.fr),该协会与格勒诺布尔阿尔卑斯大学和格勒诺布尔INP有合同关系,并由法国科学院赞助。
引用这篇文章: MOREAU René, SOMMERIA Joël (2024年4月12日), 运动物体受到的阻力, 环境百科全书,咨询于 2025年1月21日 [在线ISSN 2555-0950]网址: https://www.encyclopedie-environnement.org/zh/physique-zh/drag-suffered-moving-bodies/.
环境百科全书中的文章是根据知识共享BY-NC-SA许可条款提供的,该许可授权复制的条件是:引用来源,不作商业使用,共享相同的初始条件,并且在每次重复使用或分发时复制知识共享BY-NC-SA许可声明。









