潮汐

潮汐是指海平面周期性变化的过程,周期通常是半天(接近12小时),但在某些地区是一天。潮汐由月球引力引起,在一定程度上也受太阳吸引,潮汐幅度会随月相和不同的天文周期而变化。沿海局地猛烈的洋流也与潮汐有关。除了这些众所周知的局地作用之外,潮汐通过促进海水的垂直混合而影响全球气候。潮汐振荡所激发的内波沿海水温差界面传播,并在波浪破裂时促使海水混合。最后,在地质时间尺度上,潮汐减慢了地球自转的速度,并使月球远离地球。
1. 自古以来的观察
古人们已经通过经验了解到潮汐与月球运动之间的联系[1]。每次潮汐中低潮(低水位)和高潮(高水位)的出现相差约25分钟,即1/60天,与月球12个小时公转1/60周(公转周期约30天)相符合。由于这个时间差,实际的潮汐间隔时长为12 小时 25 分钟。且众所周知的是,与上弦月和下弦月(春潮)期间相比,在满月和新月(露潮)期间的潮汐更猛烈。这表明潮汐主要受制于月球,而受太阳的影响则较小。潮汐在二分日时特别强烈,其强度取决于距月球的距离,由于月球公转轨道是椭圆形的,该距离还存在约10%的波动。地表某特定位置的潮汐振幅由潮汐系数描述,根据天文周期的不同,潮汐系数在20-120范围内变化。
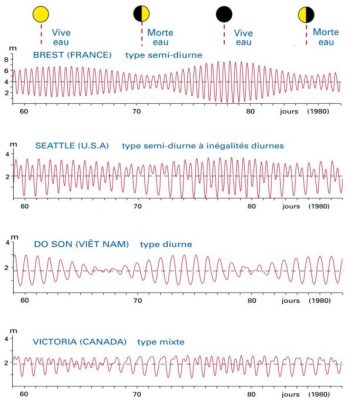
(图中:Vive eau-活水;BREST(FRANCE) 法国布雷斯特;Morte eau-死水;type semi-diturne 半日潮型;SEATTLE 美国西雅图;type semi-diturne à inègalites diurnes 不规则半日潮型;DO SON (Viètnam) 越南涂山;type diurne 全日潮型;VICTORIA(CANADA)加拿大维多利亚; type mixte 混合潮型;jours 天数)
潮差是指高低潮之间的潮位差,很大程度上也取决于地理位置。在加拿大魁北克翁加瓦湾、英国塞文河口和法国诺曼底圣米歇尔山,最高潮差分别达到18米、16.5米和15米,但在其他地区,最高潮差通常为几十厘米。另外,正如图1[2]中的曲线所示,这一显著的半日潮震荡在大西洋海岸比较典型,但并非在每个地方都可以观察到。我们在下文中将回到这一点。
由于弹性作用,地球的固体部分也存在潮汐效应,但幅度仅为10厘米级别。我们在海边观察到的,即为海洋潮汐与陆地潮汐之间的这种差异。之前的测量是在岸边用浮标测量的,最近用超声波或雷达水位探测器取代。测高卫星现在可以通过雷达测量,在通过GPS跟踪位置的浮标进行校准后,绘制整个海洋表面的潮汐图。
2. 牛顿静力学理论
潮汐很早就被解释为月球和太阳的引力效应。但是,这种解释与海面不仅在一天中面向月亮时升高,在背对月亮时也升高,且周期是12小时(而不是24小时)的事实相违背。艾萨克·牛顿(1643-1727)在1687年发表的著作《自然哲学的数学原理》中,通过万有引力理论首次解释了这一悖论[3]。潮汐是地表上受地外引力影响最为显而易见的现象,因此具有重要研究价值。
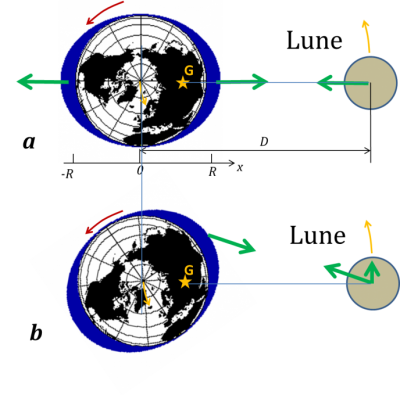
牛顿首先通过作用力和反作用力定律表明,如果地球引力使月球沿一定轨道旋转,那么月球一定会对地球施加大小相等、方向相反的力。因此地球也算是绕月球旋转,更精确地说是围绕它们的引力中心(图2上的G点)旋转。地球上的每个部分都与地球一起绕这个中心旋转,就像宇航员在沿轨道飞行的飞船附近会保持无重力状态、与飞船共同飞行一样。其原因就是每个物体在重力场中都会受到与自身质量无关的、大小相同的加速度。因此,使海洋相对于地面运动的原因不在于月球对海洋的引力场,而是该引力场与月球对地球重心的引力场的差值。更靠近月球的一侧引力更大,而距离较远的另一侧则较小,从而在两侧都涨潮(见图2)。另一个等效的论证是将自己置于以月球轨道角速度围绕该重心旋转的参考系中:离心力随后补偿了地球中心的月球引力,但它在月球对面的点上占主导地位,而引力在月球一侧占主导地位。这分别导致了两个凸起。
根据牛顿静力学理论,假定涨潮位置相对于地-月系统位置固定,则在地球自转时,地面上的某点在一天中能先后经过两个涨潮位置,导致每天有两次高潮,因此潮汐周期为半天。
当太阳和月球同升同落(新月)以及太阳和月球位于对立方向(满月)时,由于两侧海面上升的现象,在月球对潮汐影响的基础上,补充考虑太阳对潮汐的影响。这个补充解释了所观测到的春潮与露潮的交替出现的现象。太阳的引力比月亮大,但由于地日距离更大,太阳在近日侧和远日侧形成的引力场差异较小,因此,引力吸引随距离的平方减小,而相应的潮汐效应随距离的立方减小。
3. 潮汐幅度变化
由于地球自转、地球公转和月球公转轨道平面不同,导致潮汐更加复杂多变。其中地球自转轴相对于地球公转轨道平面倾角为23°26’,且公转轨道平面接近月球轨道所在平面(相对于地球公转轨道平面倾角为5°9’)。图2的图示严格适用于二分日,当旋转轴横向于太阳的方向,在大潮时与月亮对齐时。
然而,地球的自转轴在“至暑点”和“至寒点”朝向或背离太阳,而在二分日均匀受太阳直射。我们可以通过假想地球自转轴与公转轨道平面的倾斜角度为90°的极限情况来说明:即地球的自转轴在二至日时会沿着地-日连线指向太阳,那么则有地球上任意一个点的高度将不再随旋转而改变的结论。另一方面,在二分日时,自转轴会与两侧涨潮位置的连线垂直,则地球上的某点点将围绕它旋转,而高度没有任何变化,就像橄榄球围绕其主轴旋转一样。地球上的某点将能连续通过潮涨和潮落为位置。因此活水的潮汐在二分日强于二至日就可以理解了。
最后,由于月球的轨道不是圆形,而是椭圆形,月球到地球的距离D在近地点(最小)和远地点(最大)相差约10%,因此近地点的潮汐效应比远地点强30%(与1/D3成正比)。在建立潮汐表时,需要非常精确地考虑这些不同的天文效应。在整个19世纪和20世纪,对潮汐的理解和预测一直是许多工作的主题(重点1),因为它对航行和沿海使用具有根本的兴趣和重要性。
4. 潮汐波
牛顿静力学理论假设海洋的两侧涨潮位置相对于月球固定,因此潮汐能够以地球自转反向速度传播,赤道处的速度将达到450 米/秒。但由于海洋表面的形变,这种传播速度被限制在约200 米/秒以内(图2b)。该速度通过公式c=(gd)1/2与海洋深度d和重力加速度g相关(https://www.encyclopedie-environnement.org/eau/vagues-houles/)。这就产生了c=200 米/秒,平均深度为d=4000米。因此,这种波滞后于月球的位置,这导致了凸起的移动,如图2b所示。
此外,海岸的形状也极大地限制了潮汐传播,海洋盆地就像潮汐冲刷形成的水池一样。已经发现的一些潮汐的波动形式,有点类似于乐器中声波的振动。
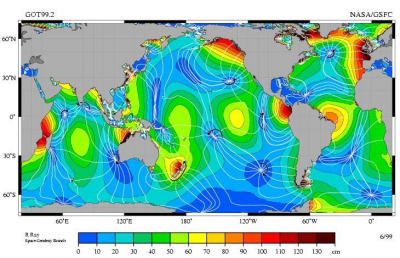
牛顿力学作为潮汐驱动力的原理仍然是准确的,但潮汐的具体结果取决于上述传播现象以及潮汐的激发频率与海洋盆地的自然振荡频率一致时的共振现象。
目前,使用高空卫星可以将潮汐振幅的测量误差控制在一厘米以内(如图3)。我们从图上可以看到振幅大小的多变性,红色表示振荡的峰值,蓝色表示振幅为零的振荡节点。图上的等潮差线表示潮汐峰值与月球到达天顶时的延迟。潮汐波垂直于这些线传播,即围绕某个节点旋转。由于地转偏向力,这样的旋转在北半球是逆时针方向。
不同天文效应对潮汐的调制更准确地表示为不同时期的激励之和,然而半日模式占主导地位。这就是这种模式,称为M2,如图3所示。注意波腹之间(或节点之间)的平均距离对应于8500公里量级的潮汐波长,即波浪在12小时期间以速度c=200米/秒行进的距离。
在昼夜周期也有一种应激反应,这是由于两个相对的吸引力凸起的轻微不对称造成的。这种被称为M1的模式被迫达到比M2弱20倍的水平,但它实际上与太平洋产生了共鸣,太平洋的大小与其波长相当,约为15000公里。因此,在太平洋的一些地区,昼夜潮汐非常显著。位于M2模式节点上的地区,如越南,则主要感受到这种M1模式(图1中的第三条曲线)。另外,区域显示了M1和M2模式的叠加(图1中的第2条和第4条曲线)。

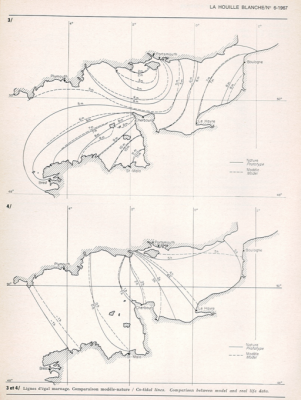
潮汐波经常在海湾或内陆海(如英吉利海峡)被放大。这是因为能量传播得更多缓慢地,与深度的平方根成正比,导致在恒定通量下能量密度的增加:从5000米移动到50米从而使能量密度增加10倍,即振幅增加3倍。在英吉利海峡,平均振幅通常从离岸1米增加到3米,潮汐与强流有关。流入的水流在地转偏向力的作用下转向法国海岸,并在退潮时离开,这会放大法国一侧的潮差,对英国一侧不利。这些效果可以在位于英吉利海峡的入口的大型“科里奥利”旋转平台(如图4所示)。因此,整个英吉利海峡的潮汐幅度和相位可以被复制(图5).
当前的数值模型能够在1cm的精确度内,模拟重现并预测这些潮汐现象。其中主要的困难是如何量化在湍流条件下海床的摩擦以及激发内潮时的能量损失(参见本文第5节)。
5. 对海平面的其他影响
潮汐不是影响海平面的唯一因素。首先,我们可以想象一下在通常几米高波浪的海洋中进行厘米测量的可能性。事实上,即便水位波动很大,几平方公里内的平均水位足以很好地代表当地水位。此外,对于图3中的潮汐振幅,仅过滤并保留了给定的时间段(12小时 25分钟),类似于接收无线电波需要选择频率。因此,没有考虑其他频率作用的影响。
在这些其他影响中,大气压力是相当直接的影响因素。局部高压会降低水位:1 千帕的额外高压通过简单的静力平衡就能使重量为10 3 牛顿/平方米的水柱水位降低10厘米。相反,低压能提高水位。在飓风的中心,大气压为91.3 千帕时,水面能够抬升1 米的高度。这种水位的抬升增强了沿海地区海浪和暴雨造成的破坏。
另一种破坏是由于风的摩擦力造成的。当它远离海岸时,这股力量使水位降低,反之则将水推向岸边。有暴雨时可以产生约1米高的海浪。这些现象与大潮同时发生能够破坏防御工事,导致洪水泛滥,例如2010年2月袭击法国的辛西娅风暴,或2005年8月袭击新奥尔良的卡特里娜飓风。然而,这些取决于风和大气压的现象比能够导致山洪爆发的局部猛烈降水要容易预测。
从长远来看,由于海洋扩张,在全球变暖的局势下,平均海平面将继续上升,其中海洋扩张占海平面上升原因的65%,冰川融化占剩余的35%。最近的测量结果表明,海平面平均每年升高2毫米。
最后,海岸线的水位也取决于地球固体部分的演化。泥沙通过淤积或侵蚀改变了海岸线。由于大型河流上的水坝减少了河流中的泥沙输入,因此侵蚀作用目前倾向于占主导地位。由于密西西比河带来的泥沙减少,路易斯安那州海岸受到海水的严重侵蚀。由于几百万年来大陆的漂移,深层地质运动也对海岸线形状的改变有一定影响。在加拿大和欧洲北部,最显著的地质影响就是冰盖融化的地壳反弹,由于10,000年前冰盖的融化,斯堪的纳维亚半岛的沿海水位每年上升几毫米。这种水位升高引起周边地区的下沉(如布列塔尼),譬如7000年前竖立在陆地上的竖石纪念碑如今被淹没在7m深的海水中。
6. 利用潮汐的能量
自中世纪以来,潮汐工厂就一直在有利的地点利用潮汐能量,如在波涛汹涌的河口或小海湾处修建水坝。1967年投入运行的法国朗斯潮汐发电厂采纳了这个方法,利用了兰斯河口的大坝,以及可在涨潮和退潮时双向运行的定向叶片涡轮机。其总装机容量为240兆瓦,平均运行容量为57兆瓦,发电量占布列塔尼市的45%,供电量占3.5%。投运45年以来,它一直是世界上最大的潮汐发电厂,直到2011年规模更大的韩国四华湖(Sihwa Lake)电厂建成投运(装机容量254兆瓦)。
但是,有大潮的地点很少允许建造这种规模的设施,并且出于保护自然景观的需要,目前更难临海建立。曾经有一个宏伟的项目拟在潮汐振幅极大的圣米歇尔山(Mont Saint-Michel)建立大坝,但在19世纪70年代遭到放弃,政府转而支持核电发展。
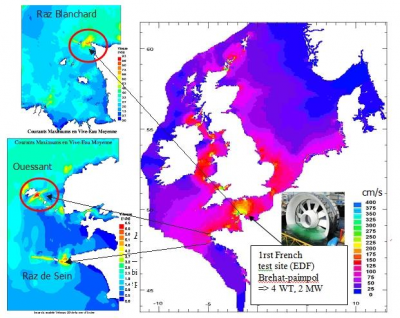
目前的趋势是直接使用潮汐带动水力涡轮机以及海面上的风力涡轮机,产生电流。这些涡轮机不需要水库,因此对环境的影响较小。但其发展目前仅处于装机容量几兆瓦的初始阶段,仅在苏格兰和布列塔尼设有试点(见图2)。苏格兰的目标是到2020年建成年产1,000 兆瓦的水力发电场。欧洲的总装机容量估计能达到10,000 兆瓦(平均运行容量5,000兆瓦),其中80%位于法国和英国。这相当于法国电力平均消耗量的约10%。
这一资源仅占潮汐耗散的总功率的0.2%,类比于通过地球自转而消耗的功率(参见第8节)。能源提取趋向于减缓潮流,从而在局部降低其振幅,从而减小粘滞摩擦损失。可以预期,提取的能量将在没有捕获的情况下以热的形式散失。然而,很难计算对地球自转的回馈影响,而这影响非常微小[5]。
7. 内潮汐
海水密度随深度而增加,浅层海水比深层海水温暖(因此密度较小)。这样的密度分层也可能由盐分导致,例如由直布罗陀海峡进入地中海的海水会由于密度较低而停留在浅层水域。这种情况可以总结为不同密度产生的双层模型。
内部波振荡(通常称海洋内波)可以与表面波相似的方式沿着密度层的分界面传播。然而,受两层之间密度差异的影响,海洋内波的传播速度要慢得多通过用减少的重力gδρ/ρ代替重力g来描述,其中δρ/ω是相对密度两层之间的差异。因此,在厚度为H的表层中,波的传播速度为c=(Hgδρ/ρ)1/2。此时在厚度为100 米的海水表层,内波的传播速度仅为表面波传播速度的1/30倍,约为1米/秒。

如图7所示,潮汐在整个水面上引导水平的海流。但是,经过坡面时,该海流会获得一个使界面变形的垂直分量,从而产生一个海洋内波,在这种情况下称为内潮汐。其波长约为100 千米(在12小时的潮汐周期内以1米/秒的速度行进的距离)。而且它们倾向于作为孤立波,位于高振幅的紧凑波中。尽管这些波在深层水域传播,但他们通过传递波形改变海面的亮度,以至于在海洋表面即可观察到其产生的水平海流(图7)。
在海洋的许多地方都能观察到内潮汐的产生。最活跃的地方之一是位于台湾与菲律宾之间的吕宋海峡,由中国南海的一个水下山脊产生垂直位移超过300米的海洋内波。这些波浪破坏即消散,促进了海水的垂直混合,进而影响了海洋的总体环流和气候(参见本文第6节)。
8. 天文效应和能量耗散
在天文时间上,潮汐以每世纪2毫秒的幅度延长一昼夜的长度并推动月球以每年3.8厘米的速度离开。地球自转的减慢目前可以很精确地通过原子钟测量,以2亿年的时间长度衡量,一昼夜的时间大约延长一个小时。地球到月球的距离可以直接通过由阿波罗登月任务发射的反射器所发送的激光脉冲的往返时间测量,测量精度可达1厘米[7]。
对于珊瑚化石的观测证实了地球自转的减慢[6],其环纹圈数可以计量一年的天数。因此,距今4亿年前的每年是410天,每天是21.5小时。根据满月确立的历月数同样表明一年多于13个月,即月亮的旋转速度更快(因此离地球更近)。
这些影响可以通过图2b的图表理解。地球的自转会使两侧涨潮位置偏移,因此与牛顿静力学模型不一致。来自月球的引力施加了使地球减速的扭矩并为月球带来能量。这样的能量会驱离月球,因而减缓其公转速度(与1 /√r成正比)。然而,由地月之间的距离r和速度相乘所得的月球动量矩却增加(与√r成正比)。地球的动量矩则以相应的比例减小,因此总动力矩保持不变。地月间的总机械能降低,通过潮汐的方式,在洋流过程中转化为热量而耗散。
天文测量可以精确确定旋转能量的减少,从而推断出潮汐运动消耗的总功率为2.9 ×10 12 W。海洋学家以往估计的功率消耗约为该数值的一半,其中大多数功率消耗在沿海地区。剩下的一半功率,现在可确定为由于激发内潮汐产生的“遗漏耗散”(参见第5节),在海洋深处扩散并最终消散。这种由海浪破裂引起的消散,导致海水的缓慢垂直混合。这些因素对热盐循环的影响正在积极研究中。
参考资料及说明
封面图片:Mont-Saint Michel, où les marées peuvent atteindre un marnage de 15m. source https://upload.wikimedia.org/wikipedia/commons/thumb/2/29/Mont-Saint-Michel_Drone.jpg/1280px-Mont-Saint-Michel_Drone.jpg.
[1] http://www.imcce.fr/promenade/pages5/525.html#Para02
[2] Tidal level records at more than 900 sites over the world are available on http://www.ioc-sealevelmonitoring.org/
[3] Newton I. (1687) ’Philosophiae naturalis principia mathematica’
[4] http://science.nasa.gov/media/medialibrary/2000/06/15/ast15jun_2_resources/oceantides.gif
[5] Maitre T., http://encyclopedie-energie.org/notices/les-hydroliennes
[6] This statement needs to be qualified, as a large energy extraction would in turn change the shape and phase of the tides, and thus the torque exerted on the Earth. nevertheless, a 5,000 MW extraction represents just 0.2% of the total power dissipated in the tides (see section 8)
[7] http://culturesciencesphysique.ens-lyon.fr/ressource/laser-distance-terre-lune.xml
[8] Runcorn S.K. , « Corals as paleontological clocks», Scientific American, vol. 215, 1966, p. 26–33
环境百科全书由环境和能源百科全书协会出版 (www.a3e.fr),该协会与格勒诺布尔阿尔卑斯大学和格勒诺布尔INP有合同关系,并由法国科学院赞助。
引用这篇文章: SOMMERIA Joël (2024年3月9日), 潮汐, 环境百科全书,咨询于 2025年1月21日 [在线ISSN 2555-0950]网址: https://www.encyclopedie-environnement.org/zh/eau-zh/the-tides/.
环境百科全书中的文章是根据知识共享BY-NC-SA许可条款提供的,该许可授权复制的条件是:引用来源,不作商业使用,共享相同的初始条件,并且在每次重复使用或分发时复制知识共享BY-NC-SA许可声明。







