| Focus 2/2 | Traînée subie par les corps en mouvement

Le sillage turbulent

PDF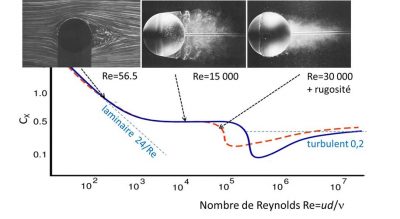

Décollement sillage sphère nombres Reynold - sillage - encyclopédie environnements
Figure 1. Décollement d’un sillage derrière une sphère à différents nombres de Reynolds, représentés sur la courbe du coefficient de trainée : à Re=56,5, l’écoulement se détache à l’aval mais reste laminaire ; à Re=15 000, l’écoulement est turbulent mais sa couche limite reste laminaire ; à Re=30 000, la couche limite est déstabilisée par un fil fin collé sur la sphère, reproduisant ainsi le comportement à Re≃106 trop rapide pour être visualisé. La tige visible à droite est le support de la sphère [Source : Documents Werlé Onera et van Dyke, Album of fluid motion]
La Figure ci-contre illustre, sur le cas emblématique d’une sphère, comment le sillage passe d’un régime laminaire à un régime de plus en plus turbulent lorsque le nombre de Reynolds augmente.

Pour une valeur modérée, Re=56,5, on voit que les trajectoires se décollent de la sphère mais seulement sur sa partie aval, contrairement à l’écoulement symétrique obtenu à très faible Re (voir Figure 2 de l’article). Ce décollement affecte encore peu le coefficient de traînée dont la loi reste proche de celle du régime laminaire en 24/Re, comme on le voit sur la courbe bleue.

A plus grand Re, l’écoulement est constitué à l’amont d’une fine couche cisaillée enveloppant la surface de la sphère, appelée couche limite, tandis qu’à l’aval il est turbulent. Le sillage, visualisé par l’injection de fumée, occupe une large section transverse, correspondant à un coefficient de traînée assez grand CX≃0,5, valeur quasi-constante lorsque Re est compris entre 103 et 105.

Au-delà de Re=105, la traînée chute bizarrement puis se stabilise à une valeur proche de 0,2. On peut reproduire cette chute à plus faible Re en perturbant la couche limite par une rugosité ou un fil annulaire collé sur la sphère, ce qui est le cas de la photo de droite, à Re=30000. On voit alors que la couche limite devient elle-même turbulente, et ceci a pour effet de retarder son décollement, conduisant à un sillage plus étroit. C’est l’explication de la chute du coefficient de traînée.

C’est pour produire une telle réduction de traînée que les balles de golf ne sont pas lisses mais alvéolées : pour une vitesse de 50 m/s et un diamètre de 4 cm, on a Re=2 105, et on peut voir sur la figure que pour cette valeur, la trainée pour une sphère rugueuse (pointillé rouge) est en effet inférieure à celle d’une sphère lisse.

Le cas des très grands nombres de Reynolds peut être vu comme le cas limite d’une très faible viscosité. Un fluide possédant une viscosité strictement nulle glisserait sans frottement sur l’obstacle, et son écoulement représenterait une sorte d’idéal où l’amont et l’aval seraient symétriques et laminaires, et où la traînée s’annulerait. Cette limite théorique n’est cependant jamais atteinte, ce qui est constitue le paradoxe de D’Alembert. L’explication tient au fait que la viscosité, aussi faible soit-elle, produit toujours une couche limite, plus épaisse à l’aval qu’à l’amont, ce qui impose une dissymétrie entre amont et aval. Par ailleurs, à très faible viscosité, la couche limite devient instable et alimente la turbulence du sillage, conduisant à la valeur limite non nulle de la traînée que l’on observe aux très grands nombres de Reynolds.