Le refroidissement vient du ciel

Le pouvoir refroidissant d’une surface exposée au ciel provient du déséquilibre entre le rayonnement thermique émis et le rayonnement reçu du ciel – ou, pour être plus précis, de l’atmosphère. Le rayonnement [26] correspond aux molécules de l’atmosphère excitées thermiquement. Cette émission thermique dépend de la température et de la concentration des molécules ainsi que de leur distance au sol. Elle correspond à une émission infrarouge centrée sur 10 µm.

1. Loi de Kirchoff et corps noir

L’excitation thermique des atomes et des molécules de la matière les fait vibrer, tourner et entraîne l’émission d’un rayonnement électromagnétique. Considérons d’abord un matériau de température et de composition uniformes appelé « corps noir » qui absorbe et donc émet toutes les radiations selon la loi de Kirchoff (Lire : Le rayonnement thermique du corps noir).

2. Loi de Stefan-Boltzmann et émissivité du matériau

La puissance radiative totale P émise par un élément de surface à la température absolue T peut être obtenue en intégrant la radiance spectrale du corps noir sur toutes les longueurs d’onde et sur un demi-espace au-dessus de la surface. On obtient la formule bien connue P = σT⁴ où P est en W.m^-2 et T en K ; σ = 5,670×10^-8 W.m^-2. K^-4 est la constante dite de Stefan-Boltzmann.

Pour les matériaux qui n’absorbent ou n’émettent pas toutes les radiations, appelés « corps gris », la loi de Stefan-Boltzmann ci-dessus doit être corrigée par ce que l’on appelle l’émissivité du matériau (Le rayonnement thermique du corps noir). L’émissivité a la même valeur que l’absorptivité car les deux grandeurs correspondent aux processus symétriques d’émission et d’absorption de la lumière entre deux états d’excitations moléculaires [27]. Pour un corps gris avec une émissivité ε < 1, la loi de Stefan-Boltzmann ci-dessus devient P = εσT⁴.

Notons cependant que lorsque la rosée commence à se former, le substrat est mouillé par l’eau. C’est alors l’émissivité de l’eau qui importe. L’émissivité de l’eau est proche de l’unité (0,98 dans la fenêtre atmosphérique, voir ci-dessous en section 3).

3. Émissivité de l’atmosphère. Température du ciel

L’atmosphère dont les molécules absorbent dans des bandes spectrales spécifiques et émettent des rayonnements dans la partie à ondes longues du spectre (3-100 µm) est un corps gris. L’oxygène et l’azote, qui composent l’atmosphère à environ 99 %, n’absorbent ni n’émettent de rayonnement dans l’infrarouge lointain ; seule compte la contribution de la vapeur d’eau (environ 0,2 % à 2 % en volume) et du dioxyde de carbone (environ 0,03 % en volume). Le rayonnement de la vapeur d’eau est donc le plus important. La forte absorption dans cette région spectrale correspond à un corps noir à une température d’environ 300K, à l’exception d’une absorption plus faible entre 7 et 14 µm. Cette dernière est connue comme la fenêtre atmosphérique et ne contient aucune contribution de l’eau. Seul un pic dû à l’ozone stratosphérique est présent, dont l’influence est relativement faible en raison de la basse température de la stratosphère. La concentration de vapeur d’eau diminue généralement avec l’altitude, ce qui fait de la couche limite atmosphérique [28] l’endroit où la plupart des radiations IR sont émises vers le sol. La couche limite s’étend de quelques dizaines de mètres à quelques kilomètres.

On peut également définir une température apparente du ciel T_s, qui relie la température de l’air au sol T_a et l’émissivité du ciel ε_s pour donner la même radiance S du ciel vu du sol, par. On peut facilement déduire la température du ciel.

4. Refroidissement par déficit radiatif

Le déficit radiatif R est la différence entre la puissance radiative du matériau de surface en condensation émise vers le ciel et la puissance envoyée par l’atmosphère lorsqu’elle est exposée à un rayonnement de ciel clair. Avec la température du matériau T_c ≈ T_a, la température de l’air, on a :

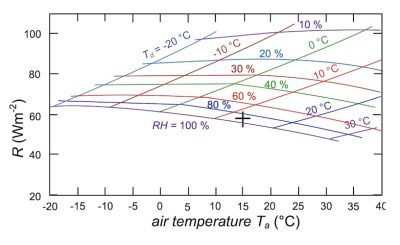
Puisque et les matériaux se refroidissent en dessous de la température de l’air. R est donc la puissance de refroidissement disponible pour la condensation de la rosée. Comme l’émissivité du ciel dépend principalement de la teneur en vapeur d’eau de l’atmosphère, le déficit radiatif peut être exprimé en fonction de la température du point de rosée T_d  ou de l’humidité relative RH (définie dans le Focus Air humide et condensation). Dans la figure 1, Bliss (1961 [29]) décrit le déficit en fonction de T_a pour plusieurs humidités relatives de l’air RH et T_d. Pour des conditions nocturnes typiques où la rosée se forme (T_a = 15°C et RH = 85% – 90%, T_d = 12,5 °C), R ≈ 60 W.m^-2.

5. Dépendance angulaire

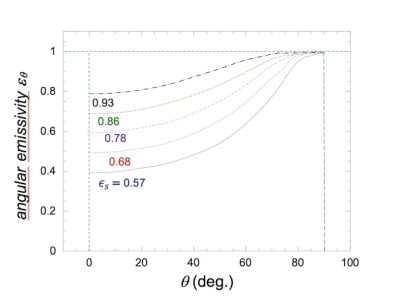
L’émissivité estimée ci-dessus est l’émissivité totale du ciel où tous les angles et toutes les contributions de longueur d’onde ont été additionnés. Il existe cependant une dépendance marquée de l’émissivité du ciel avec l’angle zénithal [30] θ (figure 2), .

ε_s est l’émissivité totale. L’émissivité est la plus faible pour l’atmosphère vue près de la verticale (θ = 0 – 30°) correspondant au plus petit trajet lumineux, et la plus élevée, proche de l’unité, près de l’horizontale (θ = 75 – 90°). Pour un refroidissement radiatif efficace d’une surface terrestre, tous les angles inférieurs à environ 15° au-dessus de l’horizontale doivent donc être évités. À partir de la dépendance de l’émissivité du ciel par rapport à l’angle, l’influence de l’angle d’inclinaison par rapport à l’horizontale du matériau de refroidissement peut être évaluée [31]. Sans surprise, le déficit radiatif est maximal pour la position horizontale et minimal pour la position verticale.

---

Notes et références

[26] La RADIATION est l’émission d’énergie par des ondes électromagnétiques.

[27] ÉTATS D’EXCITATION MOLÉCULAIRE : Un état excité d’un atome ou d’une molécule est un état quantique avec une énergie plus élevée que le minimum, l’état fondamental (c’est-à-dire plus d’énergie que le minimum absolu). Les excitations, par exemple par l’absorption de lumière (un photon), augmentent le niveau d’énergie au-dessus d’un point de départ choisi, l’état fondamental ou un état déjà excité. Le retour à un état moins excité correspond à l’émission d’un photon (lumière) dont la longueur d’onde dépend de la différence d’énergie des deux états. Pour une excitation thermique à température ambiante, la gamme d’énergie correspond à des longueurs d’onde infrarouges

[28] LA COUCHE LIMITE ATMOSPHÉRIQUE comprend la partie la plus basse de l’atmosphère qui s’étend depuis le sol. C’est l’endroit où le sol et l’atmosphère échangent des chaleurs radiatives, sensibles et latentes (Voir : Pression, température et chaleur). Elle s’étend jusqu’à l’endroit où se forment les cumulus, ce qui marque le début de l’atmosphère libre. Dans cette couche, de nombreuses grandeurs physiques (vitesse d’écoulement de l’air, température, humidité…) présentent des fluctuations rapides et turbulentes et le mélange vertical est fort. L’épaisseur de la couche limite, h, peut aller de quelques dizaines de mètres à quelques km et varie avec le temps. Elle peut être exprimée par la formule suivante où H est exprimé en km, T_a est la température de l’air et T_d la température du point de rosée près du sol : H = (1/8) (T_a – T_d).

[29] BLISS R. A. (1961). Atmospheric radiation near the surface of the ground. Solar Energy 5 (3), 103–120

[30] BERGER, X., BATHIEBO, J. (2003). Directional spectral emissivities of clear skies. Renewable Energy 28 (12), 1925–1933.

[31] HOWELL, J.C., YIZHAQ, T., DRECHSLER, N., ZAMIR, Y., BEYSENS, D., SHAW, J.A. (2021). Generalized Nighttime Radiative Deficits. Journal of Hydrology 603 (B), 126971.